前言

Pytorch实现KNN近邻算法的一些思路

图像分类

图像分类是计算机视觉的核心任务，当给定我们的模型一张图片，我们的模型应该可以正确的给出图片上的物体的类别

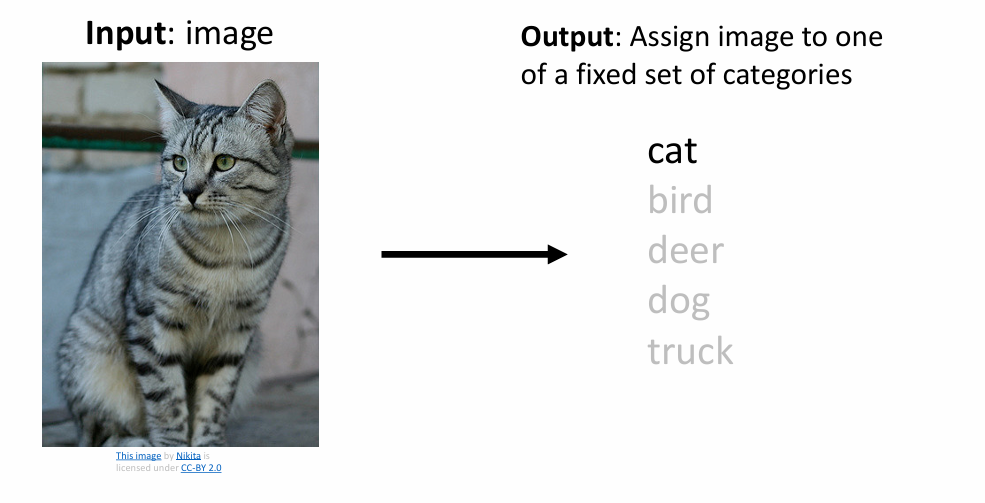
例如，图片上有一只cat,那么模型应该正确输出cat。

图像分类所面临的挑战

semantic gap 语义差异

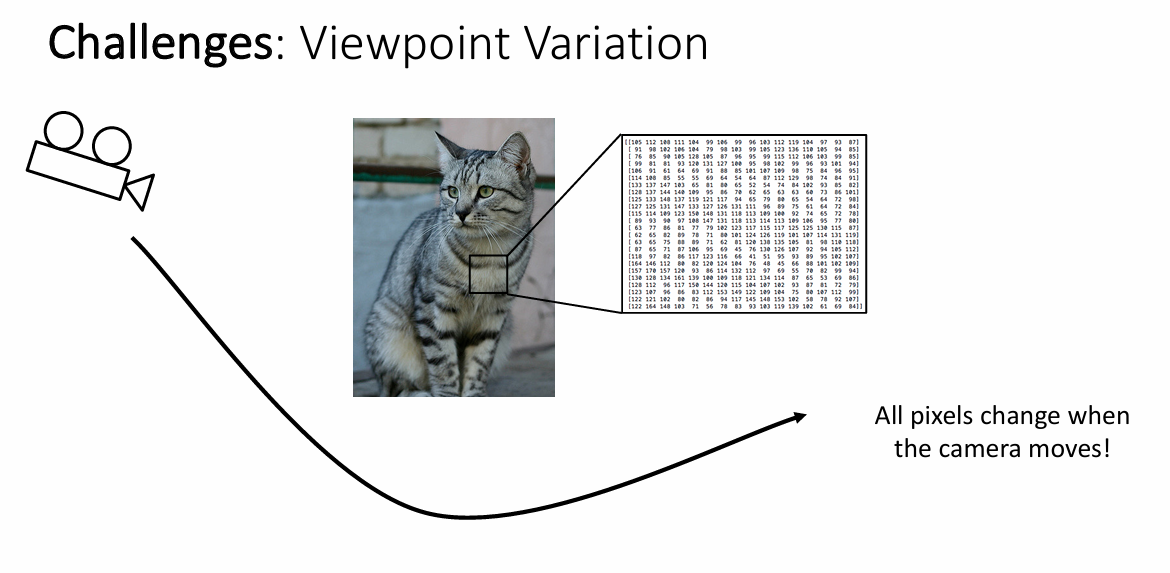
在人类看来，几乎不用思考就可以辨别出图像上的物体，但是机器却是无情的执行命令的机器，怎么把图像上所蕴含的信息传递给机器呢？于是便有了像素的表示，我们可以把一张图片细分为很多个小格子，显然，格子越多，这样图片就更加清晰，图片是以数字形式存储的，这种形式通常被称为数字图像。数字图像是由像素（picture elements）组成的矩阵，每个像素代表图像中的一个小点。所以，现在来看，这样图片就是一个数字矩阵

图像旋转

虽然可以使用矩阵和数字的方法来表示一张图片，可是，按照这种方法，当把原始图片旋转之后，每个格子内的数字就会发生变化，对于人类来说，即便是把图片旋转后，也可以很简单的辨认出图片上的物体；而对机器来说，如果不加以处理，当模型接受到一个这样的图片后，很有可能会发生错误的预测。

更多的挑战

• 不但要识别出图片中是什么，还要准确的指出它的类别。例如，照片中是一只猫，但是，是橘猫、布偶猫还是狸花猫呢
• 更难的，一些野生动物为了更好的适应所生存的环境，其颜色会和环境发生重叠，也就是所谓的保护色

这些都给我们带来了更多的挑战

图像数据集

这里，老师给出了常见的数据集，并且也对比了其中的图片数量级

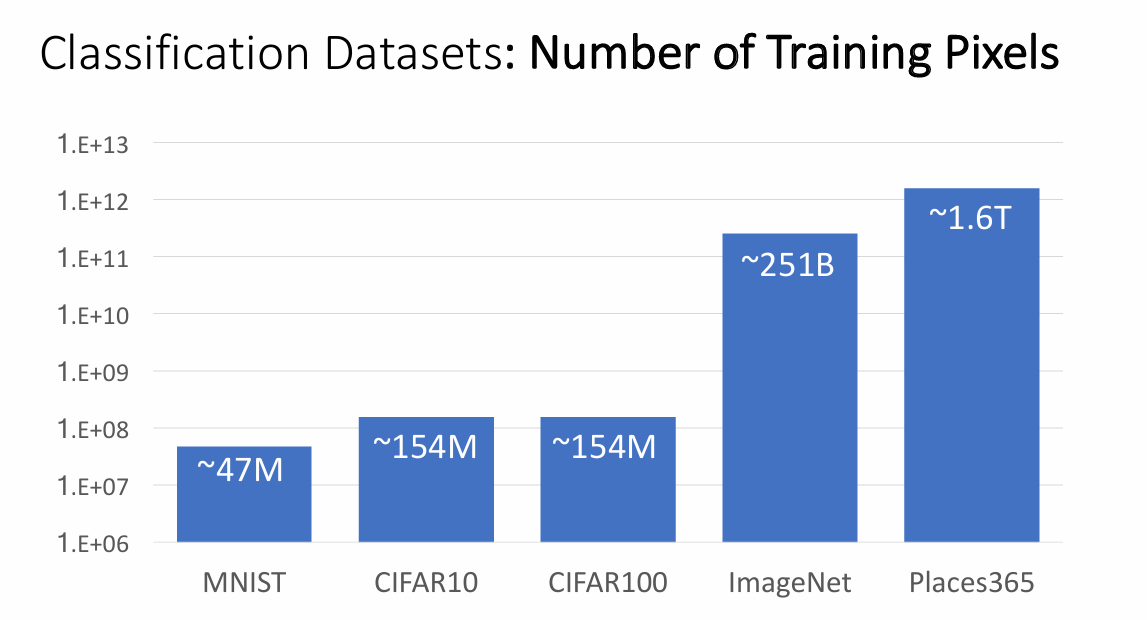
其中，我只使用过MNIST数据集(手写体数字识别)，在本次作业中实现的KNN近邻算法使用的是CIFAR10，与CIFAR100主要的区别就是总共只有10个类别，每个类别里面有很多张图片。选择这个数据库的原因是，MNIST中的数据太少，而ImageNet和Places365数据太多，折中选择了这个数据集。

KNN近邻算法

对于这类算法，一般有两个通用的API

• 训练

  1 2 3

  def train(images, labels): # To do return modle

• 预测

  1 2 3

  def predict(modle, test_images): # To do return test_labels

这个算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数都属于某一个类别，则该样本也属于这个类别。意思就是，对于一个预测的样本，如果离这个样本最近的数据都是属于A类别，那么这个要预测的样本很有可能就是A类别，毕竟它们很相似！

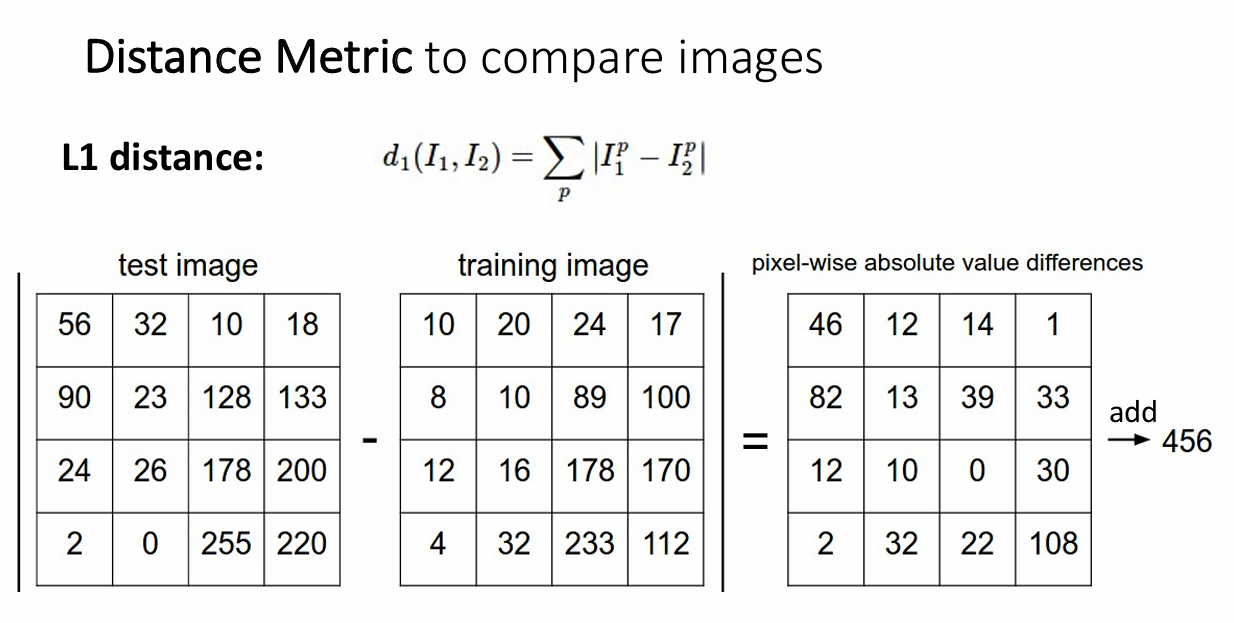
L1距离

这里的距离指的就是曼哈顿距离,计算方法就是对应坐标作差后取绝对值。

L2距离

L2距离指的是欧式距离，也就是在空间中计算两个点之间对应坐标距离的方法

代码实现

现在来实现一下上文中提到的两个API，简单起见，这里使用numpy

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

import numpy as np
class KNN:
    def __init__():
        pass
    def train(self, X, y):
        '''
        X指的是输入的训练数据
        y指的是训练数据对应的类别
        '''
        self.X = X 
        self.y = y
        
    def predict(self, X):
        # X是输入的，需要预测其类别的test数据
        num_test = X.shape[0] # 样本类别数
        Ypred = np.aeros(num_test, dtype=self.y.dtype)
        
        # 遍历所有test数据，给test数据中的每个数据找到其距离最近的那个图像
        for i in range(num_test):
            # 计算L1距离
            dis = np.sum(np.abs(X[i, :] - self.X), axis = 1)
            # 找到其中距离最近的那个值对应的index，进而获得它的类别
            min_idx = np.argmin(dis)
            # 对应的标签就是self.y的标签
            Ypred[i] = self.y[min_idx]
        
        return Ypred

这里的predict使用的是显示loop,这种情况会特别耗时！

k的取值

上面的代码没有显示的指定k的取值范围，而是直接使用k=1这个取值，首先，这样做很简单，因为只需要查看离测试样本距离最近的那个类是什么类型即可。但是，这种操作会使得算法会对异常值特别敏感，同时，不同类别之间的边界也是突出状而不是趋于平滑

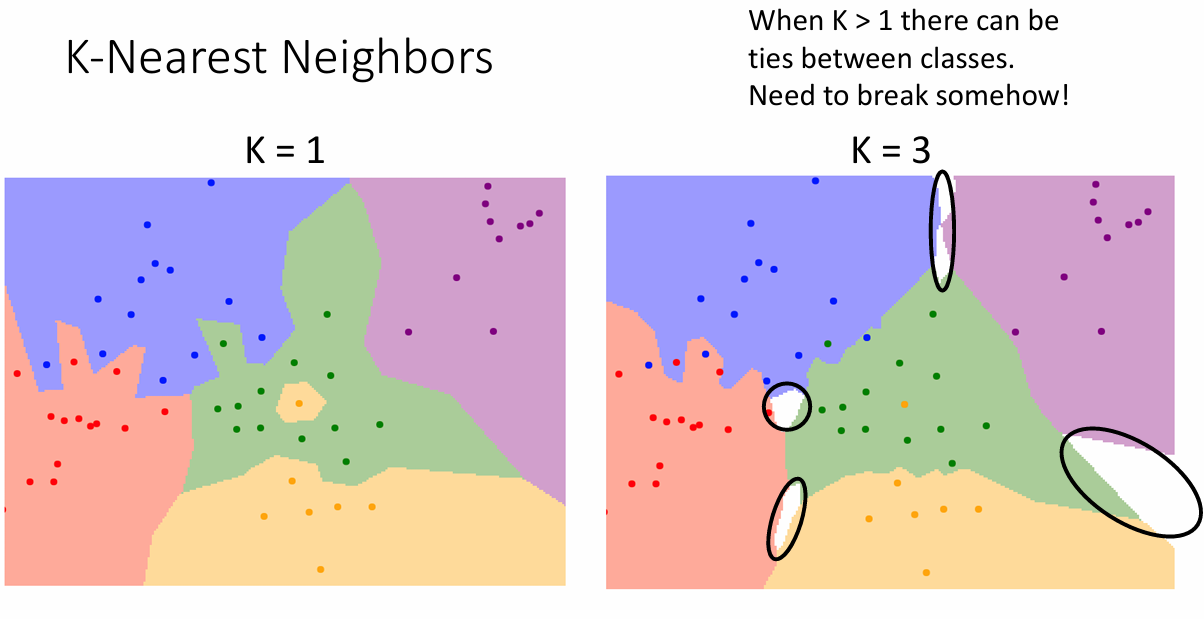
因此，我们可以提高k的取值，提高k值也减少了异常值对test数据的影响，因为test数据这次有k个不同的参考意见，而不是只去参考一个值。

使用Pytorch来实现KNN算法

首先是计算两个向量之间的距离

双重循环

This implementation uses a naive set of nested loops over the training and test data. The input data may have any number of dimensions – for example this function should be able to compute nearest neighbor between vectors, in which case the inputs will have shape (num_{train, test}, D); it should also be able to compute nearest neighbors between images, where the inputs will have shape (num_{train, test}, C, H, W). More generally, the inputs will have shape (num_{train, test}, D1, D2, …, Dn); you should flatten each element of shape (D1, D2, …, Dn) into a vector of shape (D1 * D2 * … * Dn) before computing distances.

这里是老师给的一些代码的预处理的关键提示

More generally, the inputs will have shape (num_{train, test}, D1, D2, …, Dn); you should flatten each element of shape (D1, D2, …, Dn) into a vector of shape (D1 * D2 * … * Dn) before computing distances.

对于所有的输入向量，不管是什么维度的样本，我们都可以转换为一个二维张量，这样做可以简化一些计算，同时使得结果更加清晰。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

import torch
def compute_distances_two_loops(x_train: torch.Tensor, x_test: torch.Tensor):
    """

    Args:
        x_train: Tensor of shape (num_train, D1, D2, ...)
        x_test: Tensor of shape (num_test, D1, D2, ...)

    Returns:
        dists: Tensor of shape (num_train, num_test) where dists[i, j]
            is the squared Euclidean distance between the i-th training point
            and the j-th test point. It should have the same dtype as x_train.
    """
    num_train = x_train.shape[0] # 得到行数
    num_test = x_test.shape[0]
    dists = x_train.new_zeros(num_train, num_test) # dists[i, j]是第i个x_train与x_test的距离
    x_train_flat = x_train.view(num_train, -1)
    x_test_flat = x_test.view(num_test, -1)
    for i in range(num_train):
      for j in range(num_test):
        diff = x_train_flat[i] - x_test_flat[j]
        dists[i, j] = torch.sum(diff ** 2)
    return dists

这样做十分清晰，而且不开根是因为我们不需要得到确切的欧氏距离，只是单纯的比较大小，所以直接返回距离的平方即可。

但是，这样并没有利用pytorch,会导致计算速度减慢，看看怎么优化！

一重循环

这里使用的其实是一个高级特征，通过下标索引来访问元素(熟悉numpy的肯定不陌生)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

def compute_distances_one_loop(x_train: torch.Tensor, x_test: torch.Tensor):
    
    num_train = x_train.shape[0]
    num_test = x_test.shape[0]
    dists = x_train.new_zeros(num_train, num_test)
   
    x_train_flat = x_train.view(num_train, -1)
    x_test_flat = x_test.view(num_test, -1)
    for i in range(num_train):
      diff = x_train_flat[i] - x_test_flat # 计算每个x_train与x_test
      dists[i, :] = torch.sum(diff ** 2, dim=1) # 按照行进行求和
   
    return dists

其中，diff = x_train_flat[i] - x_test_flat 这行代码可以自动帮我们计算第i个x_train与所有的x_test的差值，然后按照行的顺序进行求和(dim=1，numpy的是axis = 1)。

No loop 不使用循环

可以说不使用循环才是KNN里面一个十分精彩的部分，这里用到了高级机制BoardCast广播机制，下面我们来看一看这个部分的数学表达形式。

图片来自bilibili视频.

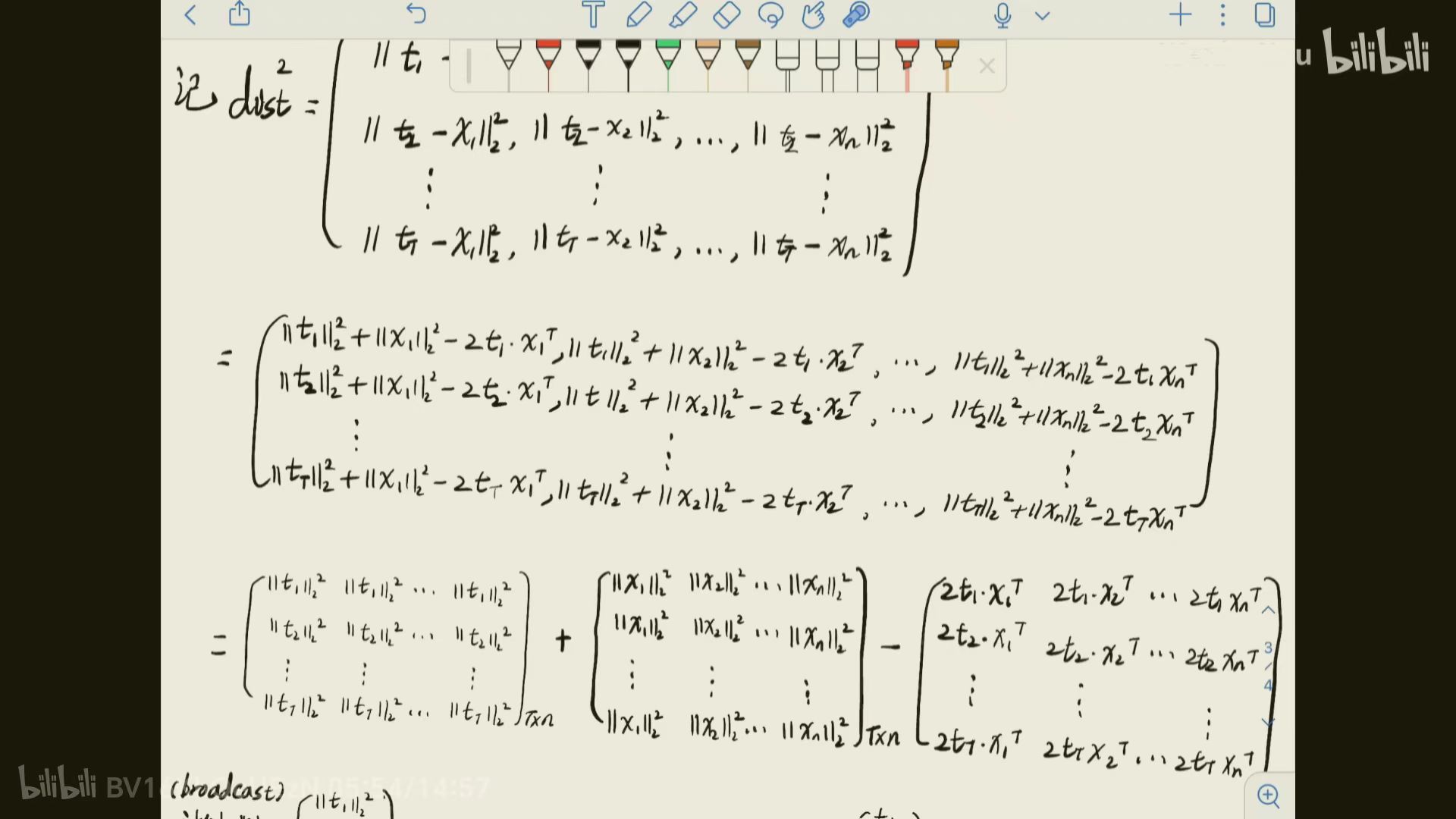
这里还需另外提醒的是矩阵的加减法，对于两个维数相同的矩阵$A 和B$，经过运算后得到$C$,其中，$$ C_{ij} = A_{ij} + B_{ij} $$

$$ C_{ij} = A_{ij} - B_{ij} $$

即对应元素相加减的操作

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

def compute_distances_no_loops(x_train: torch.Tensor, x_test: torch.Tensor):
    num_train = x_train.shape[0]
    num_test = x_test.shape[0]
    dists = x_train.new_zeros(num_train, num_test)
    x_train_flat = x_train.view(num_train, -1)
    x_test_flat = x_test.view(num_test, -1)
    x_train_squre = torch.sum(x_train_flat ** 2, dim = 1)
    x_test_squre = torch.sum(x_test_flat ** 2, dim = 1)
    # 计算点积
    temp = x_train_flat @ x_test_flat.t()
    dists = x_train_squre.view(-1, 1) + x_test_squre.view(1, -1) - 2 * temp

    return dists

根据上面的计算结果，x_train是一列的张量，x_test是一行的张量，从而两者进行广播后运算，值得注意的是，两者的内积可以转换为矩阵相乘的形式。

预测predict

在计算出每个测试样本与(x_test)每个训练样本(x_train)的距离之后，对于每个测试样本，我们就可以找到其前k个最近值，然后确定其类别后返回。

一个可能的函数看起来可能是这样的：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

def predict_labels(dists: torch.Tensor, y_train: torch.Tensor, k: int = 1):
    num_train, num_test = dists.shape
    y_pred = torch.zeros(num_test, dtype=torch.int64)
    
    for j in range(num_test): # 遍历x_test数据
        # 找到每个测试样本最近的k个训练样本的距离和索引
        dists_k, indices = torch.topk(dists[:, j], k, largest=False) # largest=False 是升序
        
        # 获取这些最近的k个训练样本的标签
        nearest_labels = y_train[indices]
        
        # 计算每个标签的出现次数并选择出现次数最多的标签
        labels, counts = torch.unique(nearest_labels, return_counts=True)
        # 记录最大出现次数
        max_count = torch.max(counts)
        # 找到出现次数是最大出现次数的那个标签
        most_common_labels = labels[counts == max_count]
        # 在计数最多的标签中选择数值最小的那个标签
        y_pred[j] = torch.min(most_common_labels)
    
    return y_pred

这个代码的思路就是，寻找距离test数据的最近的k个不同类别，返回其出现次数最多的那个类别，如果有两个类别出现次数相同，那么就返回距离最近的那个。

交叉验证

k折交叉验证（英语：k-fold cross-validation），将训练集分割成k个子样本，一个单独的子样本被保留作为验证模型的数据，其他k − 1个样本用来训练。交叉验证重复k次，每个子样本验证一次，平均k次的结果或者使用其它结合方式，最终得到一个单一估测。这个方法的优势在于，同时重复运用随机产生的子样本进行训练和验证，每次的结果验证一次，10次交叉验证是最常用的。

对于原始数据 (raw 数据)，如果全部用于训练，则无法评估模型在未见过的数据上的表现，从而无法验证模型的有效性和准确性。因此，通常会将数据划分为两部分，一部分用于训练 (train)，另一部分用于测试 (test)，从而在测试集上评估模型的表现。

在实际应用中，为了更好地选择超参数，我们会引入一个额外的数据集，称为验证集 (validation)。这样，数据集可以划分为三部分：训练集 (train)、验证集 (validation) 和测试集 (test)。

具体流程如下：

1. 训练集：用于训练模型，使模型能够学习数据的特征和模式。
2. 验证集：用于选择超参数。我们在验证集上测试不同的超参数组合，并选择在验证集上表现最好的参数设置。
3. 测试集：在完成超参数选择后，我们在测试集上评估最终模型的性能。测试集完全不参与训练和参数选择，因此可以真实反映模型在新数据上的表现。

这种三分法的优势在于，验证集用于超参数选择，而测试集则用来评估模型在未见过的数据上的泛化能力，从而避免在超参数选择过程中过拟合测试集的风险。

有关交叉验证的部分解释来自ChatGPT

交叉验证 (Cross-Validation) 是一种用于更稳健地评估模型性能和选择超参数的方法。它通过多次数据划分和训练测试来减少模型对数据划分的偶然影响。在交叉验证中，我们通常将数据划分为多个等大小的部分（称为“折”或“folds”），并在每次训练时使用不同的折组合来训练和测试模型。

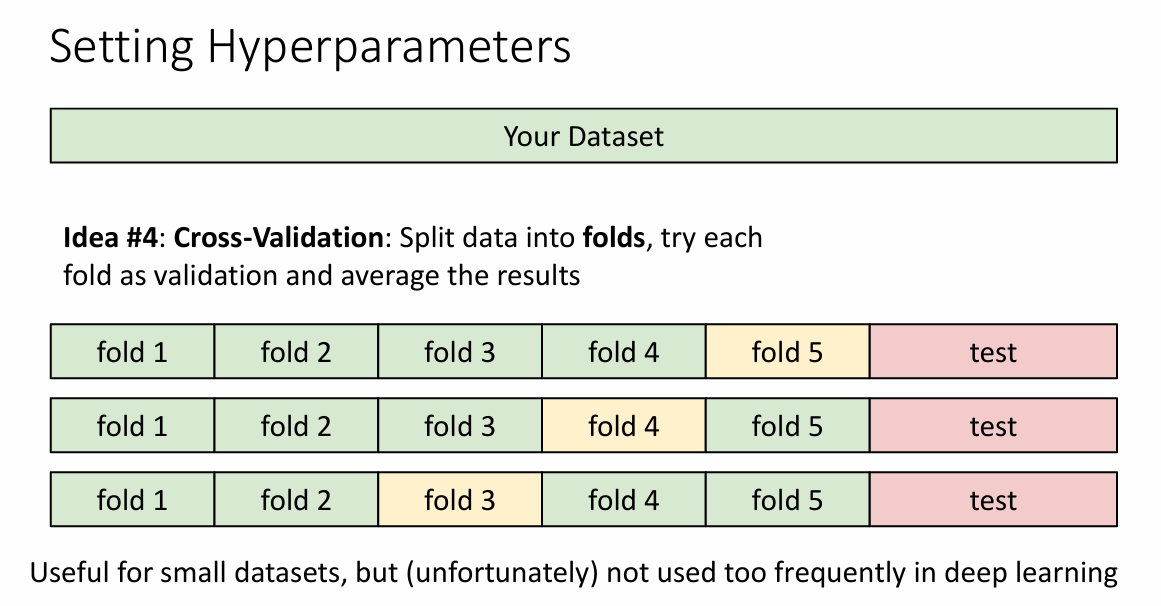
交叉验证的数据划分步骤

以常用的 K 折交叉验证 (K-Fold Cross-Validation) 为例，具体步骤如下：

1. 将数据分成 K 个等大小的折：将数据集均匀分成 K 个折，记为 fold_1, fold_2, ..., fold_K。通常，K 的值是 5 或 10。

2. 多次训练和验证：对于每次迭代（共 K 次），使用 K-1 个折作为训练集，剩下的一个折作为验证集。具体来说：

   • 第一次迭代：使用 fold_2 到 fold_K 作为训练集，fold_1 作为验证集。
   • 第二次迭代：使用 fold_1 和 fold_3 到 fold_K 作为训练集，fold_2 作为验证集。
   • 以此类推，直到每个折都被用作一次验证集。

3. 计算平均性能：在每次迭代中记录模型在验证集上的性能（例如准确率、损失等），然后将 K 次的验证结果平均，作为该模型在该超参数下的总体验证性能。

4. 选择最佳参数：对于每个超参数组合，都进行上述 K 次交叉验证，并根据平均性能选择表现最好的参数组合。

5. 最终测试：完成超参数选择后，可以在独立的测试集上评估模型的最终性能。

交叉验证的优势

交叉验证避免了简单的训练/验证分割可能带来的偶然性，使模型能更稳健地评估数据上的表现。此外，交叉验证可以最大化地利用数据，因为每个数据点都能在验证集中出现一次，同时也在训练集中使用 K-1 次。这种方法尤其适合数据量较小的场景。

总结

为了避免数据划分的偶然，我们保持三部分总体不变，对于train validation部分做出变化。

我们把上面train数据分为nums个，每一块叫做一个fold, 假设分为5个fold，对于我们的待选参数集K来说，对于第i个参数K[i]，每次都选择1个fold作为验证集(validation)，剩下的4个作为训练集，然后再计算其准确率，对于K[i]来说，我们就得到了5个不同的准确率，然后可以取平均(mean)，作为选择K[i]为参数是的准确率，最后通过准确率就可以选出最优的K。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

def knn_cross_validate(
    x_train: torch.Tensor,
    y_train: torch.Tensor,
    num_folds: int = 5,
    k_choices: List[int] = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100], # 待选K
):
    x_train_folds = list(torch.chunk(x_train, num_folds)) # 把数据拆分为 num_folds块
    y_train_folds = list(torch.chunk(y_train, num_folds))

    k_to_accuracies = {k: [] for k in k_choices} # 使用键值对进行存储

    for k in k_choices:
        for j in range(num_folds):
            x_val = x_train_folds[j] # 获取第j个验证集
            y_val = y_train_folds[j]
            x_train_fold = torch.cat([x_train_folds[i] for i in range(num_folds) if i != j], dim=0) # 剩下的num_folds作为训练集
            y_train_fold = torch.cat([y_train_folds[i] for i in range(num_folds) if i != j], dim=0)

            classifier = KnnClassifier(x_train_fold, y_train_fold)
            acc = classifier.check_accuracy(x_val, y_val, k) # 计算准确率
            k_to_accuracies[k].append(acc)

    return k_to_accuracies

总结

KNN近邻算法还是非常适合初学者入门的，其中主要难点或者说比较新鲜的点就是广播机制BoardCast以及交叉验证的代码实现！