前言
神经网络一个非常关键的地方就在于如何能够更快、更精确的求解出各种参数,这些参数一般是在学习的过程中可以得到,而有一些参数却需要人为的根据经验来进行初始化,例如学习率的大小、每次训练时batch size的大小、损失函数的选择以及激活函数的选择。下面来记录一下如何选择这些参数
激活函数
激活函数在神经网络起到的是引入非线性的作用,当我们不选择激活函数的时候,实际上并没有增加有效层的层数,而激活函数又有很多种选择,早期的激活函数有sigmoid、tanh函数,而我们用的较多的有ReLu以及ReLu的变体

类sigmoid函数
sigmoid函数在早期十分受欢迎,函数的值域在[0,1]中,这个函数在早期受欢迎的原因是它很好的模拟了神经元接受刺激产生冲动的一个过程,但是在实践中它有着很多的缺点
饱和区
当x的取值变得很大或者很小时,其值趋近于1或者0,从图中可以近似估计一下,可以看到输出$\sigma(x)$对于x的梯度近似为0,那么在使用反向传播链式求导时,很容易将上游梯度的结果变为一个非常小的值,也就是所谓的kill gradients,导致梯度不能通过反向传播而传递至前一层。

Not zero centered
从图中看出,sigmoid函数不是关于原点分布的,这就会导致在计算参数W的梯度依赖于上一层的梯度,例如,给定两个参数W1和W2,对于输出来说
$$
f = X_1W_1 + X_2W_2
$$
可以使用链式法则求得这两个参数的梯度
$$
\frac{dL}{dW_i} = \frac{dL}{df} \frac{df}{dW_i}
$$
也就是
$$
\frac{dL}{dW_i} = \frac{dL}{df} X_i
$$
而因为$X_i$恒为正(来自sigmoid的输出),所以$\frac{dL}{dW_i}$的符号只取决于上游梯度,那么对于$W_1和W_2$这两个梯度来说,其符号要么同时为正,要么同时为负,所以从图上看就是这样的

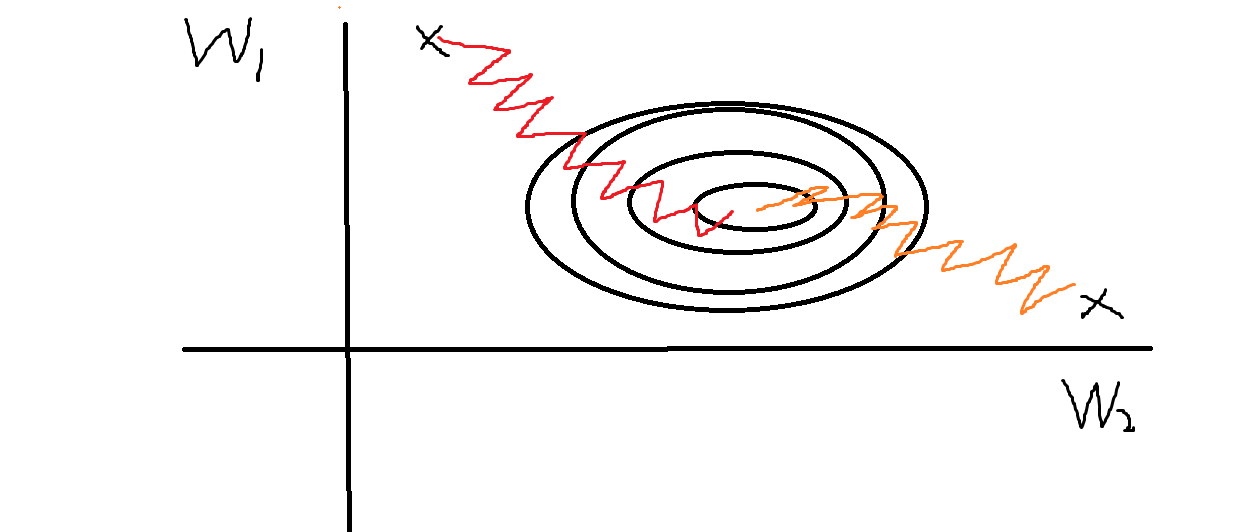
这就使得网络很难训练
计算代价高
显然,指数级别的计算代价要明显高于一般运算
tanh
这里也介绍了tanh函数,从图像上来说,与sigmoid相比,tanh只是少了not-zero-centered这个缺点

类ReLu
ReLu的激活函数是
$$
ReLu(x) = max(0, x)
$$
选择这个激活函数也是AlexNet一个创新点之一,与之前的类sigmoid函数相比,ReLu简单、收敛快、不存在饱和梯度,但是这个函数也是not zero centered,而且也有着其它的缺点
dead ReLu
当输入X小于0时,ReLu只是简单的去把X设置为0,导致小于0的部分的梯度永远也不会去更新,当输入 $x≤0$,输出总是 0。因此,如果一个神经元的输入权重和偏置的组合导致它始终进入负区,该神经元在整个训练过程中都不会被激活,也不会对学习产生贡献。也就是该神经元是dead的,并不会增强模型的能力。
为解决这个问题,研究人员又提出了ReLu的变体
Leaky ReLu
Leaky ReLu的思路是小于0的部分不是简单的设置为0,而是设置为一个很小很小的数

把设置的这个很小的数叫做$\alpha$,在反向传播中可以学习这个参数
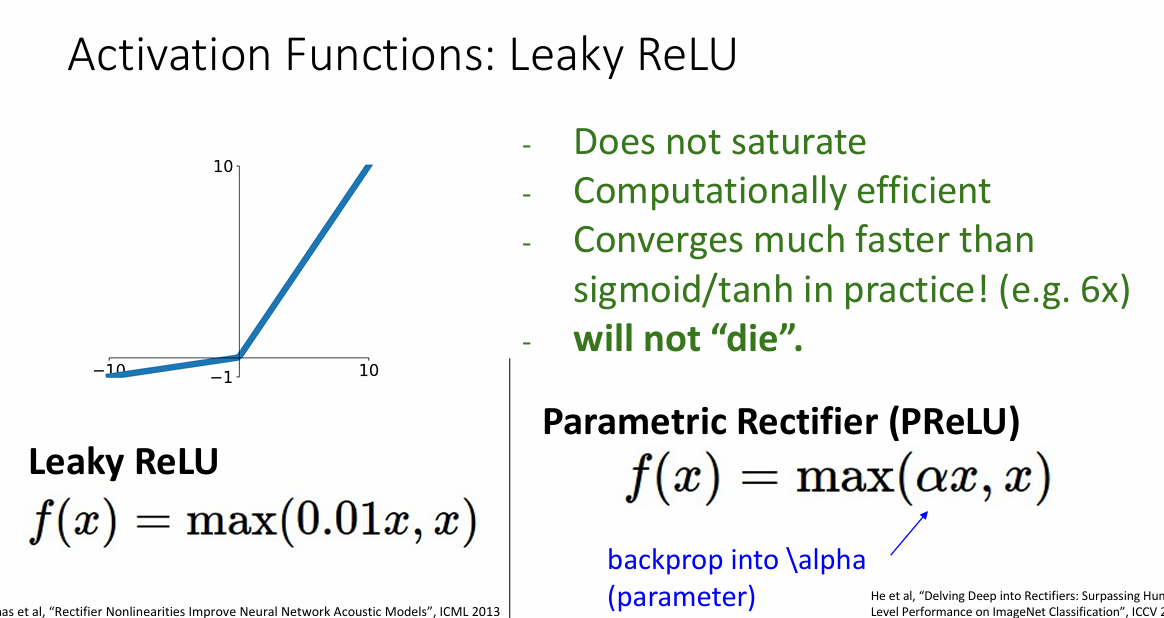
还有其它的各种变种
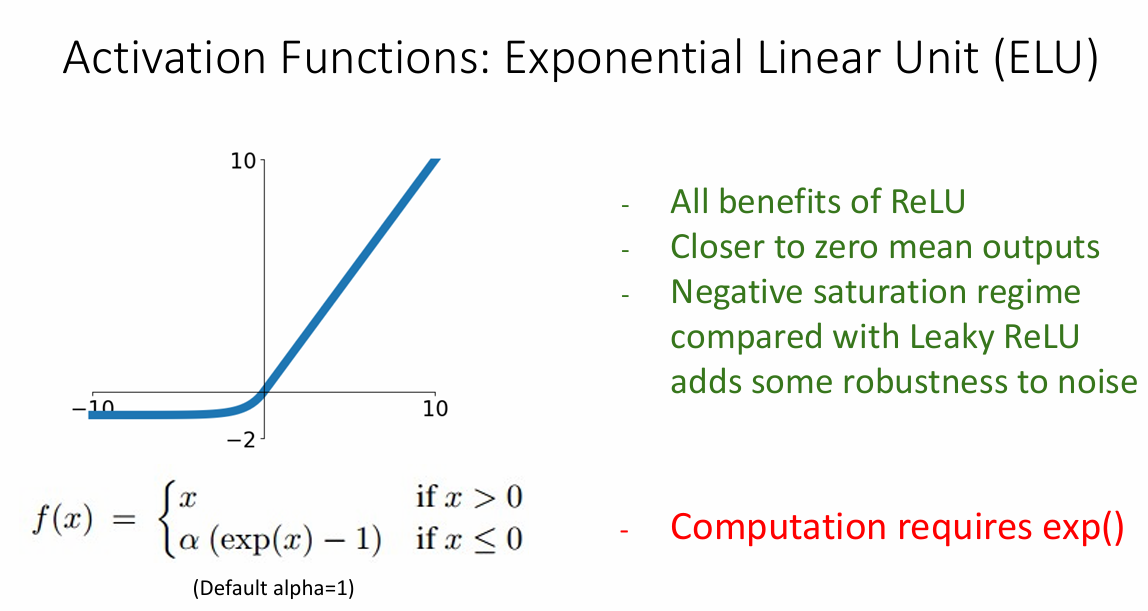
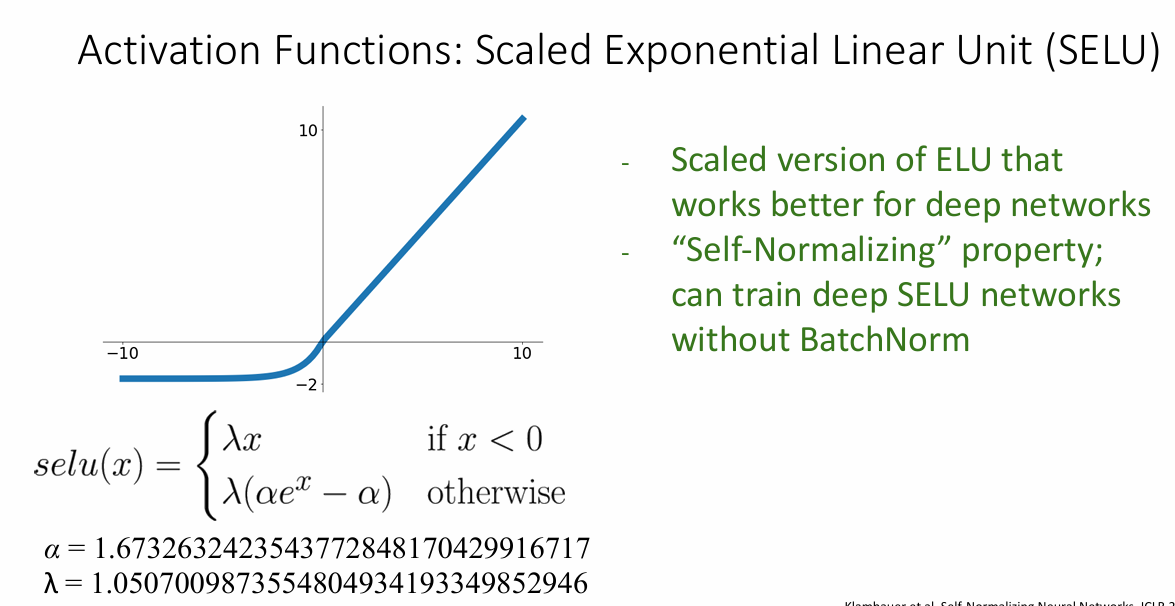
总结
规则怪谈:
- 当你不知道使用什么激活函数,或者真的不在乎那
0.1%的精度提升,直接选择ReLu - 当你需要极值的优化,那么可以尝试一下
ReLu的变体 - 不要使用
tanh和sigmoid

数据处理
对数据进行预处理可以更好的训练网络。
下图是一个对原始数据进行0-1正态分布的处理过程
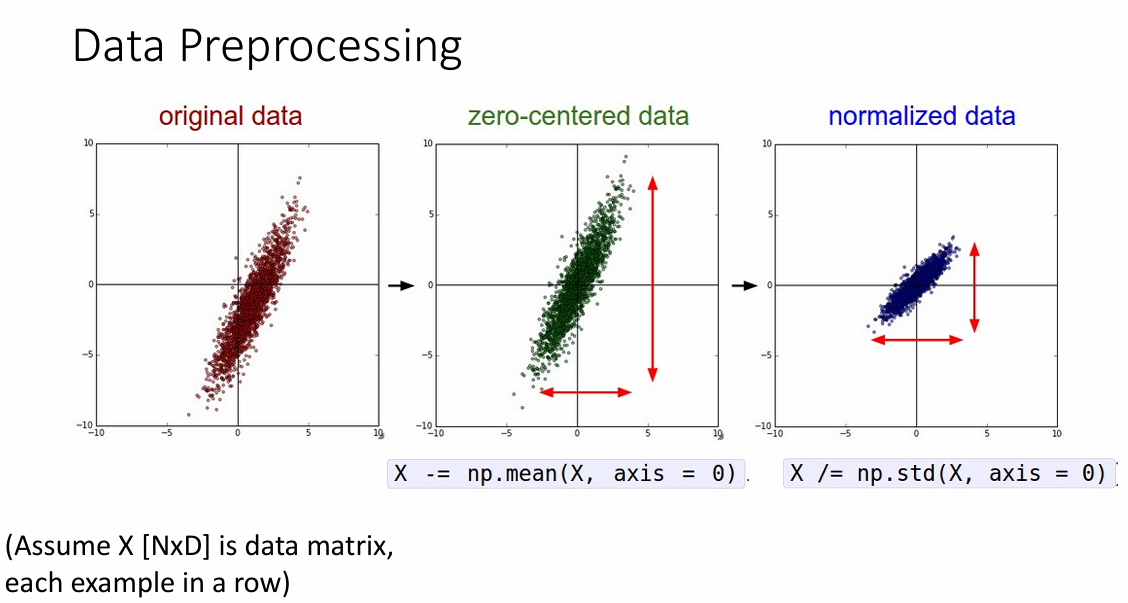
这里有一个值得注意的代码细节
|
|
这里对数据进行处理都是在同一类的数据进行处理,而在数据集里面按照一般约定,每一列是一个类的所有数据分布,所以这里是在axis=0(torch里面使用的是dim)上进行数据处理。
对数据进行预处理可以使得在反向传播时更容易求解梯度和传播梯度

对于图像来说,可以减去图片的均值、减去每个通道上的均值以及在每个通道上做正态分布初始化

权重参数初始化
到目前为止,权重参数W一直是一个非常重要的参数,而且权重的初始化也是训练网络很重要的一部分,一个想法是,假设我们有着一个比较简单的网络,如果我们把权重参数全部初始化为0
|
|
那么在前向传播的过程中,每一层的输入就都是0,那么这个网络实际上什么都做不了,一个比较常见的做法是把W按照高斯分布进行初始化
|
|
例如,weight_scale可以初始化为0.01
|
|
这样初始化在网络层数比较小的时候没什么问题,但当网络层数非常多时,后面层获得的输入就会非常非常小,以至于无法表示
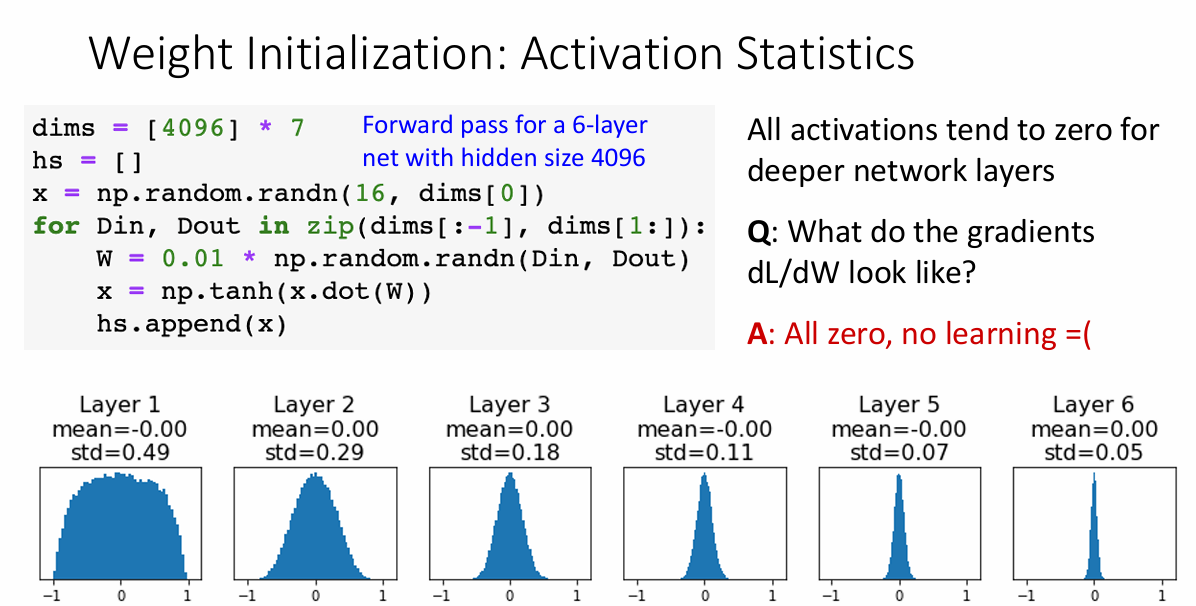
Xavier 初始化
对于激活函数是tanh时,xavier激活函数可以很好的结果这个问题,这个方法的核心思想在于把输入和输出的分布尽可能相似,也就是输入的方差与输出的方差一致。
对于输出来说
$$
y_i = \sum_{i = 0} ^ D X_iW_i
$$
为了使两者方差相等,即
$$
Var(y_i) = \sum_{i=0} ^ D Var(X_iW_i)
$$
因为输入X的方差是1,即
$$
Var(y_i) = D*Var(W_i)
$$
所以$W_i$的方差就是原来的$\frac{1}{D}$,只需要在原来初始化时除以输入维度数即可
|
|

kaiming初始化
也叫做He初始化,这个初始化方法是专门为ReLu实现的,回想一下ReLu函数,在ReLu函数作用下,对于0-1分布来说,每次产生非0的概率就是0.5,所以对于这组数据来说,每次方差都要缩小一半。
同样的,为了使输入和输出的分布近似相等,所以可以推导出在ReLu函数作用下的初始为
|
|
同样的,对于ResNet来说,整个初始化就是这样的
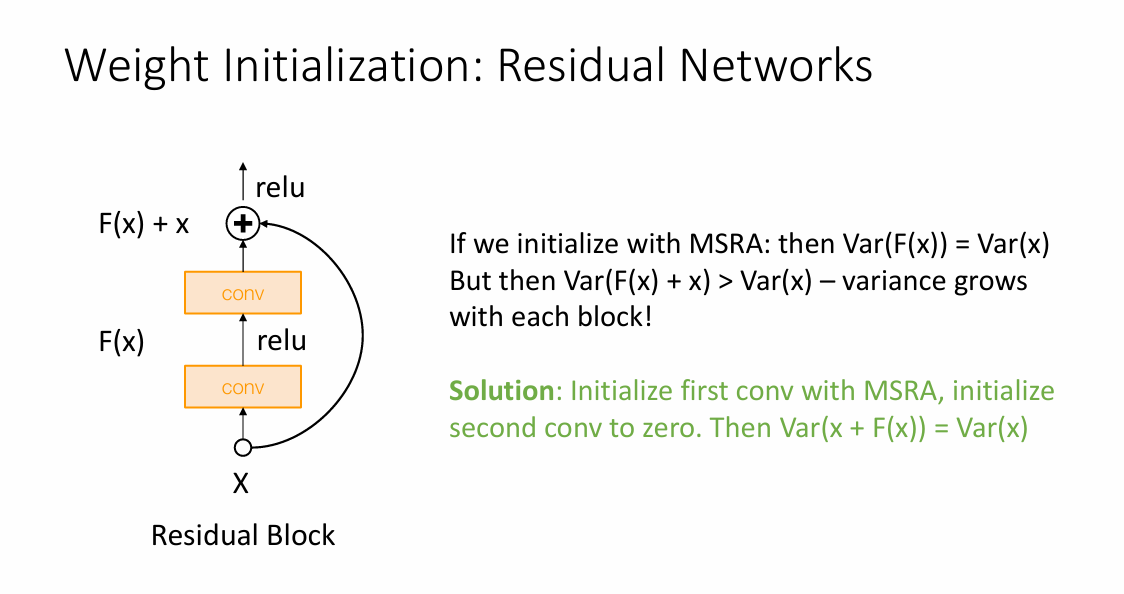
这样可以保证在两个卷积层输出后方差不变。
正则化
正则化技术是防止模型过拟合的一个关键技术,正则化可以从某种程度上减少模型的复杂度。
在一开始,对于损失函数,我们讨论了L1正则化和L2正则化这两种简单有效的正则化方法

此外老师还介绍了一种正则化方法DropOut,DropOut一般用于全连接层的优化,对于一些神经元的输出,DropOut会按照P的概率把这些神经元的输出置为0,其结果就像是在复杂的网络中选择一些简单的子网络
一样,从而降低模型的复杂度。
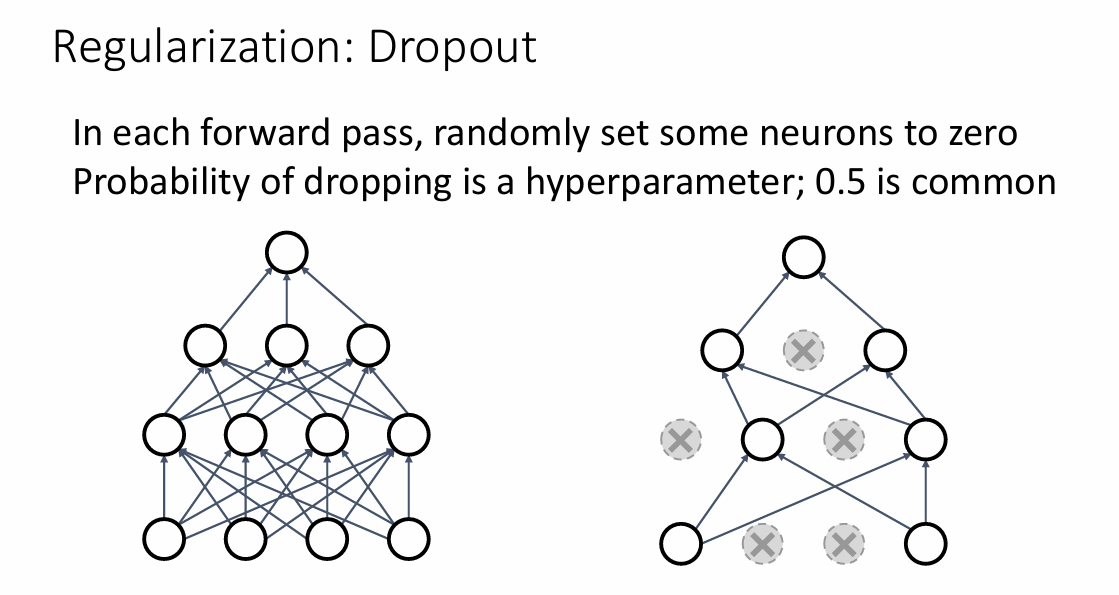
为了保证这两个模型依旧是等价的,我们把未丢弃的那些值都除以p,这样可以保证在DropOut前后两者均值相同。
数据增广
数据增广的想法可能是更好的去模拟人类的思维,对于一张图片来说,我们可以对这张图片进行裁剪、旋转、增强亮度等操作,对于人类来说,即使经过这些操作,也还是很容易就可以辨别出这是同一张图片,这恰恰也是我们对机器也可以实现的能力。
除此之外,在数据集较小、数据集图片质量不佳时,我们就可以人为的对数据进行一些操作,从而达到训练要求。
总结
这次老师分享了一些训练网络时的一些技巧,包括激活函数的选择、数据预处理的重要性、权重参数初始化的方法、正则化以及数据增广的办法,这些都会在作业中用到!