前言

好难好难

线性分类器

线性模型

线性分类器在神经网络中相当于积木的低位

你可以用很多层的线性分类器来实现一个神经网络，当然，为了提高模型拟合数据的能力，一般不会只去使用线性模型，而是会选择性的加入一些非线性模型

从线性观点

让我们继续回到上几节课提到的CIFAR10数据集，这个数据集有10个不同的类别。而对于图像的表示，我们可以把图像(input)看作一个数字矩阵，我们想要实现的内容就是，对于一个数字矩阵，能否找到一个权重参数W,使得数据的结果发生一些变化，从而根据这个输出的结果来进行分类判断。

Wx + b是一个非常经典的线性模型

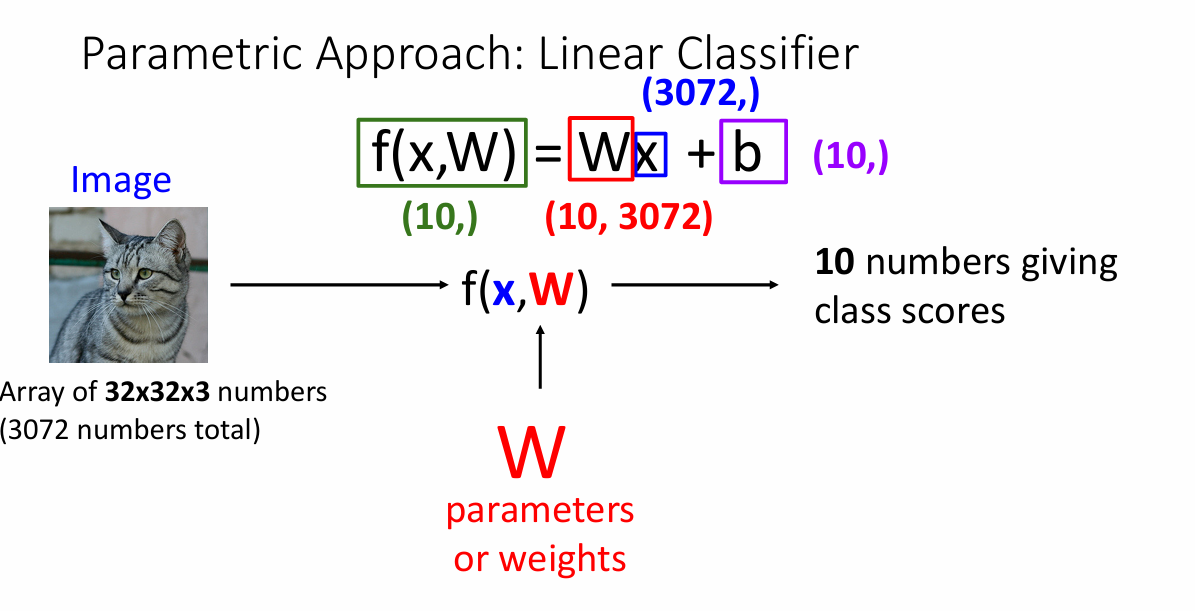
例如，对于下面这个分类问题

这里，我们假设输入的图像是一个简单的2x2的矩阵，也就是说，该图像仅仅只由4个特征点决定，那么，对于一个参数矩阵W来说，它的每一行可以看成是一个类别的权重，把这些元素对应相乘就可以得到该类别的"总分数"(例如，cat类在经过参数矩阵运算和bias之后的总分就是-96.8)。

为了使表示结果更加的整洁易懂，我们可以把这个bias添加到参数矩阵W里面。

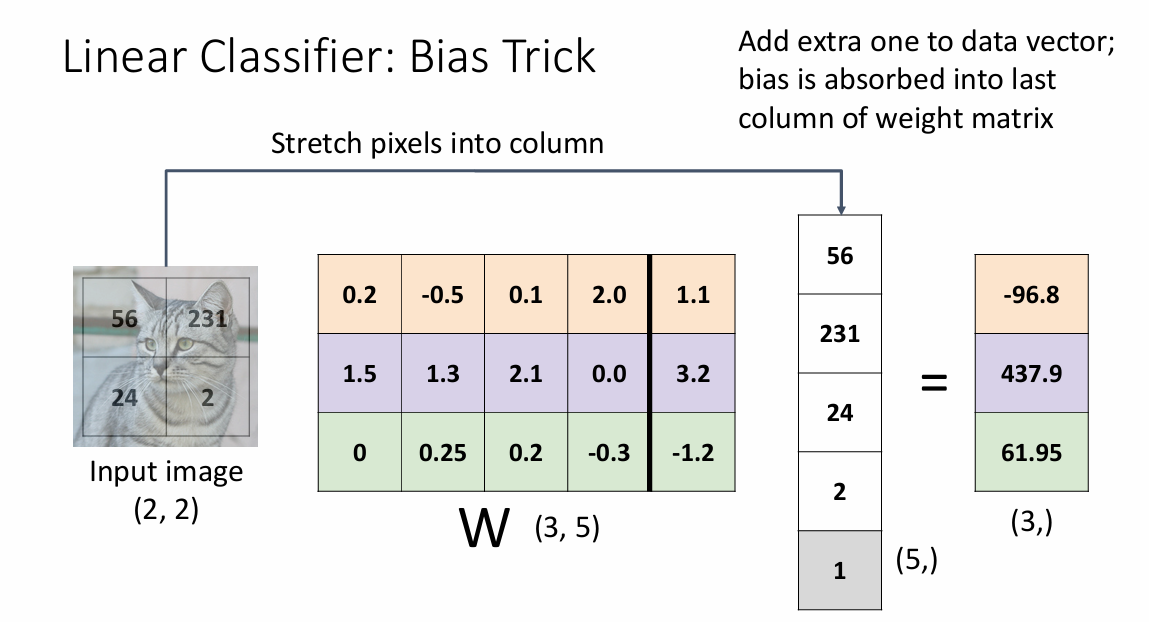
从图像观点

这里的意思就是不把输入的数据拆分为一行，而是直接调整对应元素在图像中的数值

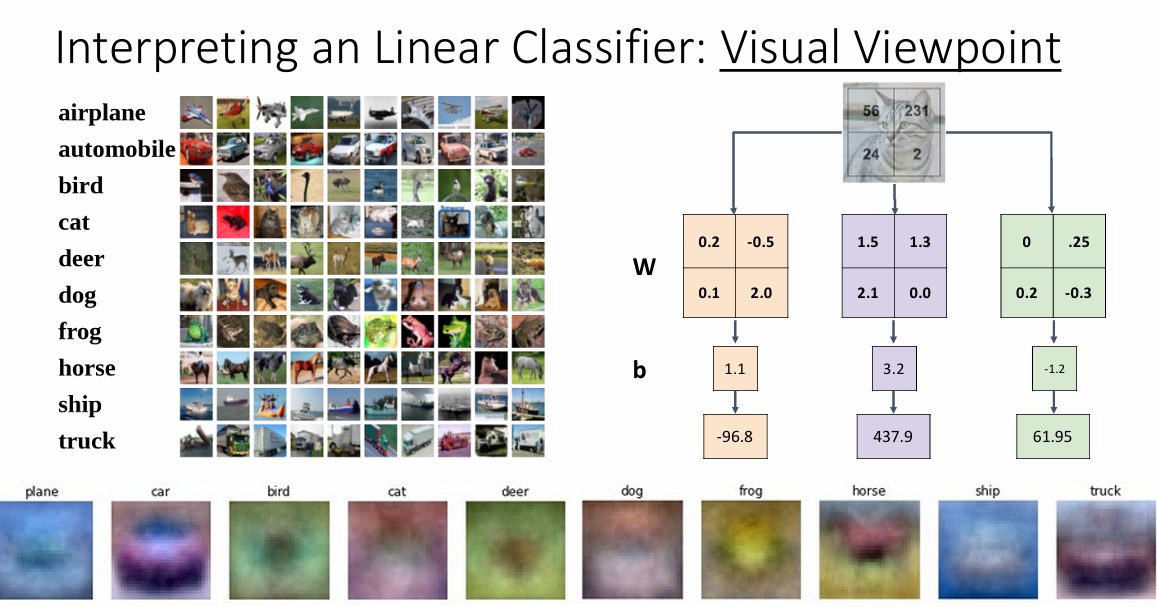
给人在视觉上的观点就是给整个图像蒙上了一层模板，有着相同背景的图片更容易被划分到同一个类别中，也就意味着，每一类别好像是有了一张模板图片一样

从几何上看

从几何上看，这些图片会被一个一个的超平面给划分切开，彼此之间没有交集

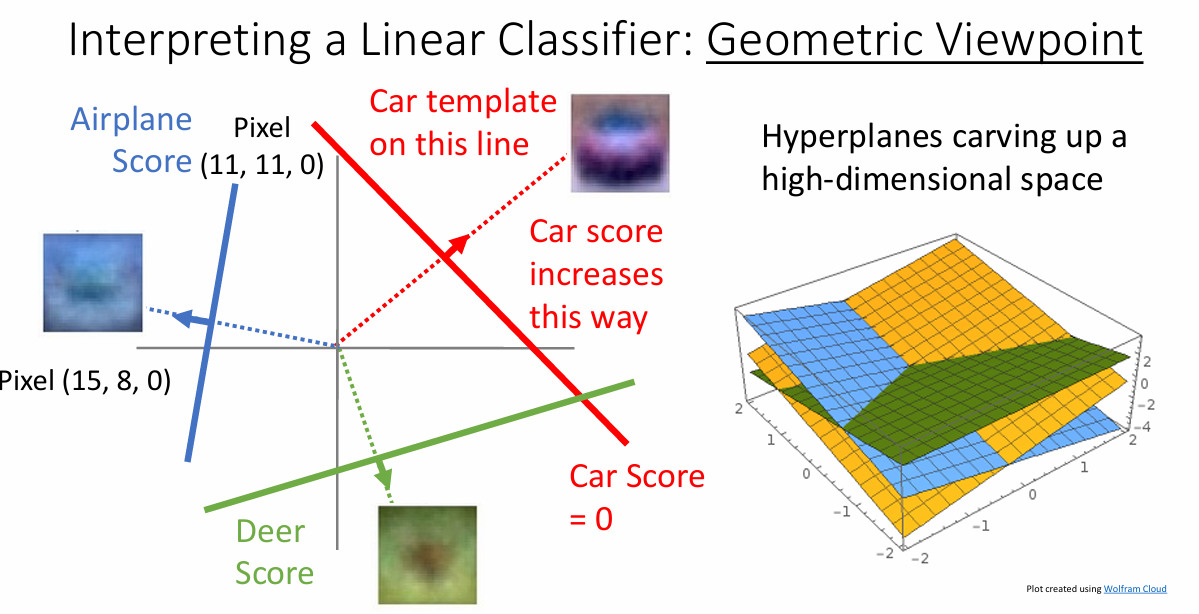
线性模型不能解决的问题

线性模型显然不太适合取解决非线性模型。这里列出来一些线性分类器不能解决的问题。

包括

一三象限问题

其实我觉得就是异或问题，对于这类问题，你无法找到一条直线来把两种颜色划分开来
非线性问题

对于这类数据一部分是呈现非线性的，除了非线性之外的数据是无法仅通过一条直线划分

下面的图片很好的表明了这些例子。

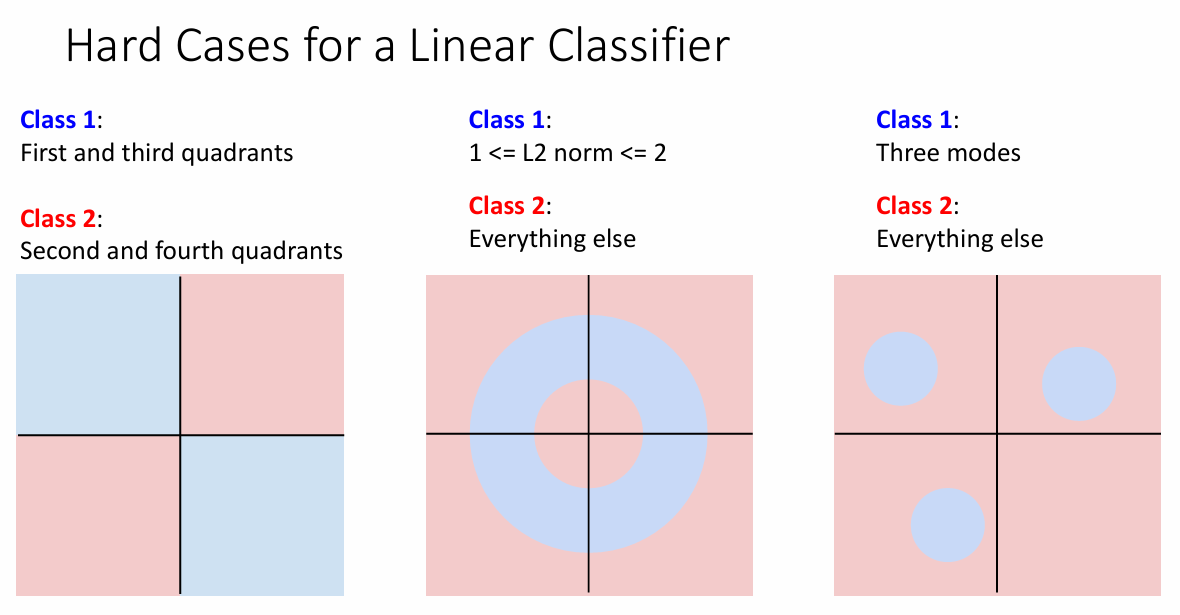
感知机不能学习异或问题！

当然，如果一层感知机实现不了，那么就再来一层！天无绝人之路！

损失函数

虽然线性模型很简单，但还是可以给我们许多启发。到目前为止，我们还没有给出一种可以更新权重W的一个方法，于是损失函数便登场了！

损失函数可以理解为一个定量来分析真实值与我们的预测值之间的偏差的一个方式，按照这种方式，当我们的预测值越接近于真实值，那么我们可以认为，在这种条件下的W是loss友好的。

另外说一点，在后续提到损失函数时，我们都更加倾向于这个损失函数是凸函数(Convex)，这样我们就可以通过导数解析的方式来求得损失函数最小时的权重W

SVM损失函数

SVM的损失函数又叫做合页损失函数(hinge loss)，在上文中，我们提到可以使用一个线性分类器来对图像进行分类

我们可以把一个这个结果S看成是线性变换后的结果，因此，对于每个图片，我们都可以通过这种方式来进行计算，从而得到它的一个分数

其中，我们很有必要来展开阐述一下这个公式

这个公式以得分输出的形式其实弱化了X W之间的关系，我们可以使用代码来进行描述

假设这里有训练集X（X: A PyTorch tensor of shape (N, D) containing a minibatch of data.),并且给出了权重参数矩阵W（W: A PyTorch tensor of shape (D, C) containing weights.）

也就是说，X的每张图片有D个特征，总共有N个样本；权重W有C个类别，每个类别有D个特征(按照列向量来说，每一个列对应一个图片)，这样，对于每一个样本X[i] (1xD)，我们都可以给这个图片计算出在不同类下面的分数

1
2
3
4
5
6
7
8


import torch
'''
X 是一个 NxD矩阵
W 是一个 DxC矩阵
'''
nums_train = X.shape[0]
for i in range(nums_train):
    socres = W.t().mv(X[i]) # 得到这个图片在所有类上的分数

就像下面这个图片一样

其中，假设X[0]是cat，那么我们就可以得到这张图片在10个类别上的对于分数;假设X[1]是car，那么我们同样可以得到car在10个类别上的分数，然后就可以得到所有的分数。

注意一些技巧，我们想要统计的是在C个类上面的分数，所以输出的张量应该是Cx1或者1xC的;torch的mv函数很好的帮助我们将一个矩阵与一个向量相乘，在数学上的感受就是一个CxD的矩阵与一个Dx1的向量相乘，从而得到一个Cx1的输出分数

再看SVM Loss

再看Loss函数，实际上做的就是一个衡量差值之间间隔的函数，方便起见，我们还是使用只有三个类和三个得分的输出

怎么计算第一个cat的损失值呢？其实就是对于元素相加减，然后再与0作比较，所以cat的loss就是

1
2
3
4


max(0, 5.1-3.2+1) +
max(0, -1.7-3.2+1)

Loss:2.9

同样我们也可以得到其它类的损失函数

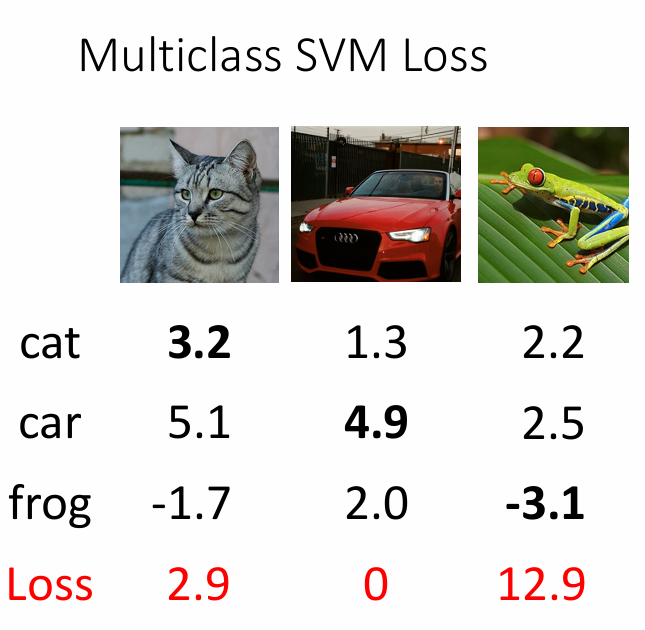
因此，这组数据的平均loss就是 Sum(loss) / x.shape[0]

同样，我们还是可以使用代码来进行描述

计算出所有类的分数

这一步我们已经计算出
找到对应正确的类，然后做加减法

得到scores后，我们可以得到这个正确的类的分数。比如，第一张图片是cat，那么我们可以找到scores中是cat的分数是3.2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


import torch
'''
X 是一个 NxD矩阵
W 是一个 DxC矩阵
y: A PyTorch tensor of shape (N,) containing training labels; y[i] = c means
      that X[i] has label c, where 0 <= c < C.
      y[i] 就是X[i]的标签类
'''
num_train = X.shape[0]
num_classes = W.shape[1]
for i in range(num_train):
    socres = W.t().mv(X[i]) # 得到这个图片在所有类上的分数
    correct_class_score = scores[y[i]] # 得到所有分数中, X[i]的分数
    for j in range(num_classes):
        if j == y[i]: # 不与自已比较
                continue
            margin = scores[j] - correct_class_score + 1  # note delta = 1
            if margin > 0: # 负分数不必相加
                loss += margin

这样我们就得到这批样本的总的loss

平均loss也可以求得

1

loss /= num_train # 样本的总loss 除以 样本的总数量

矩阵形式

经过上面的铺垫，我们就可以为后面的矩阵求导做铺垫，现在让我们把这个hinge loss的公式展开

因为我们不与自身作比较，所以，类的输出总分数就是 $$ W_j^{T} * X_i $$ 这个形式的意思就是$ W ^ T$的第j行实际上就是图像X[i]的参数，对应的，减去correct时的分数，而correct的表达可以是 $$ W_{y_i}^T * X_i $$ 然后累加和 $$ L_i = \sum_{j \neq y_i} \max(0, w_j^T x_i - w_{y_i}^T x_i + \Delta) $$ 我觉得这样写可以更加适合理解后面的梯度求导的形式！

正则化

为了防止过拟合问题，我们可以给模型的参数W来加入一些惩罚项。

首先我们来看看什么是过拟合。

过拟合

以线性回归来举例，对于训练样本中的所有数据，如果我们的模型足够大、足够复杂，那么我们的模型就可以"记住"所有的点，于是，对于一个简单的样本来说，在训练后得到的模型大概是这样的：

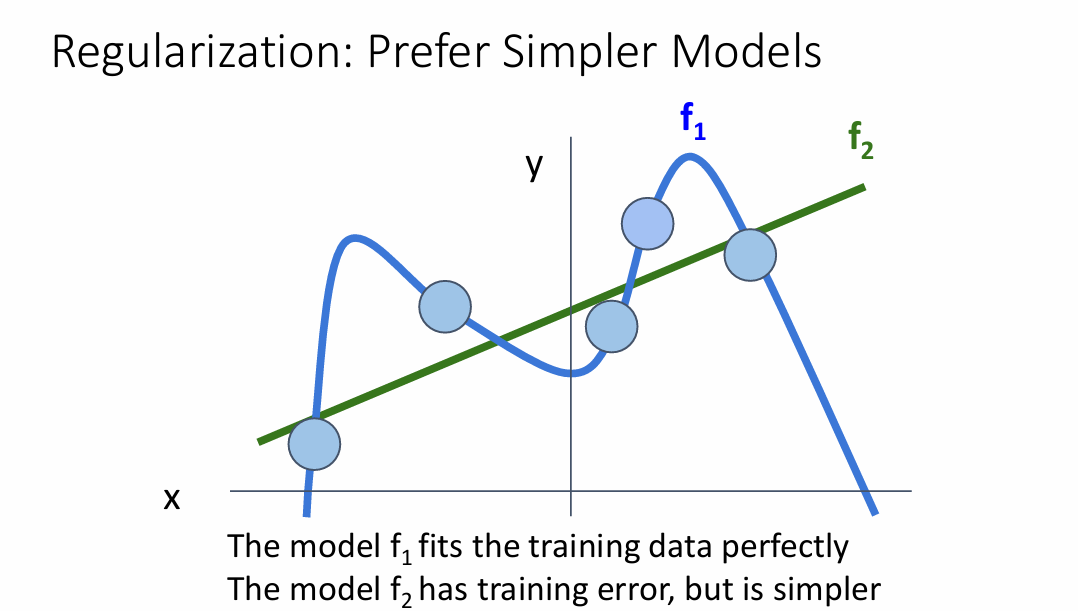
其中，f2是我们预期出现的模型性能的样子，正则化可以防止我们的模型拟合的过好，从而加强模型的预测能力。

L1 L2正则化

正则化也有着不同的类别，常见的就是L1正则化和L2正则化

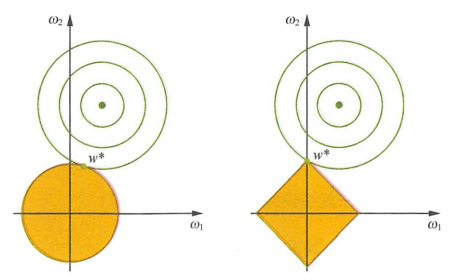
其实正则化的目的就是去把W约束在一定的解的空间内，对于矩阵W来说，越简单的模型就意味着W值的某些取值取得越小，从而拟合出来得出现呈现出一些低阶多项式的形状，当我们把W的解约定在一定的取值内，我们假设这个取值是m，对于L1正则化的那个小尾巴 $ \lambda R(W) $来说，其W的解 $$ 0 <= W_1 + W_2 + …. + W_n <= m $$ 在二维空间内，我们可以得到这个解的区域是一个菱形区域(具体的数学证明设计凸优化的知识)

同样的，对于L2正则化，我们同样要把参数W约束在一个范围内 $$ 0 <= W_1 ^ 2 + W_2 ^ 2 + ….+W_n ^ 2 <= m $$

L1 L2正则化在空间上的解释可以用下面这张图解释

softmax与交叉熵损失函数

softmax函数常用于多分类问题，对于一组输出，比如说上面cat的输出，我们可以利用这个函数把各个输出的分数转换为概率来进行研究，其数学形式长这样

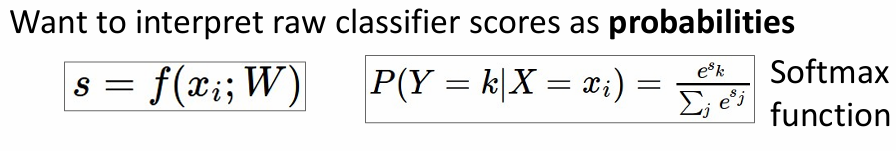
分母是各个分数转化后的总和，分子是对于该类转化后的值

交叉熵（Cross Entropy）是Shannon信息论中一个重要概念，主要用于度量两个概率分布间的差异性信息。在信息论中，交叉熵是表示两个概率分布 $p$, $q$ 的差异，其中 $p$ 表示真实分布，$q$ 表示预测分布，那么 $H(p,q)$ 就称为交叉熵 $$ H(p,q)=\sum_i p_i \cdot \ln {1 \over q_i} = - \sum_i p_i \ln q_i \tag{1} $$ 在这个问题中，对于第i类来说，其真实分布$p$的概率就是1，所以总的表达式又可以进行化简

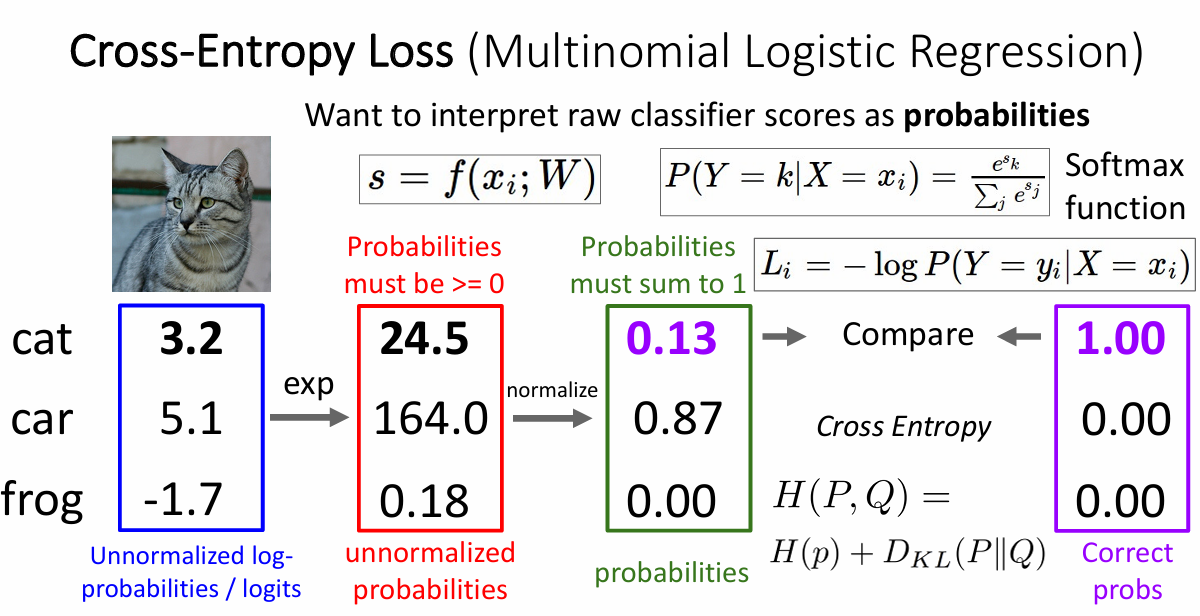
然后slices中有一个有趣的问题，当一个图片在一个有着C类的数据集上进行分类时，假设我们预测得到的这个图片是每某个类的概率差不多，那么交叉熵损失是多少？

带入公式，实际上就是 $ -log \frac{1}{C} $, 也就是 $ log C $

对于这个数据集来说，C的数量是10

总结

这次我们了解了很多损失函数和避免模型过拟合的方法，但是还没有了解怎么求得我们的最优的参数矩阵W，下次来了解一下求最优参数的方法！