前言

前面讲解了一些优化算法，尤其是各种梯度下降算法，这次来看一看神经网络

神经网络

神经网络的特点

前面我们在学习线性分类器的时候了解到，线性分类器对于异或、圆形、半圆形数据不能很好的划分出一条边界，这也导致了线性分类器不是那么的有效，而神经网络可以解决这个问题。

一般的，神经网络可以划分为输入层、隐藏层、输出层这三种结构，而正是隐藏层的一些非线性特征使得神经网络可以拟合出各种决策边界，所以在线性分类器上解决不了的问题便可以使用神经网络很好的解决。

为了简单起见，作业里面实现的是一个两层的神经网络，使用的激活函数是Relu激活函数

得分方式的改变

在之前的线性分类中，我们把 $ X^T W $看作是一个得分的输出。在神经网络里面这里的计算方式也与其计算方式相同，不同的是，在多层神经网络之间传递上一层的分数时，总是要经过非线性激活函数输出后把分数传递到下一层，这是因为如果不加激活函数，那么实际上我们在做乘法的时候还是取得是一个线性计算的过程，所以要加上激活函数，从而引入非线性。

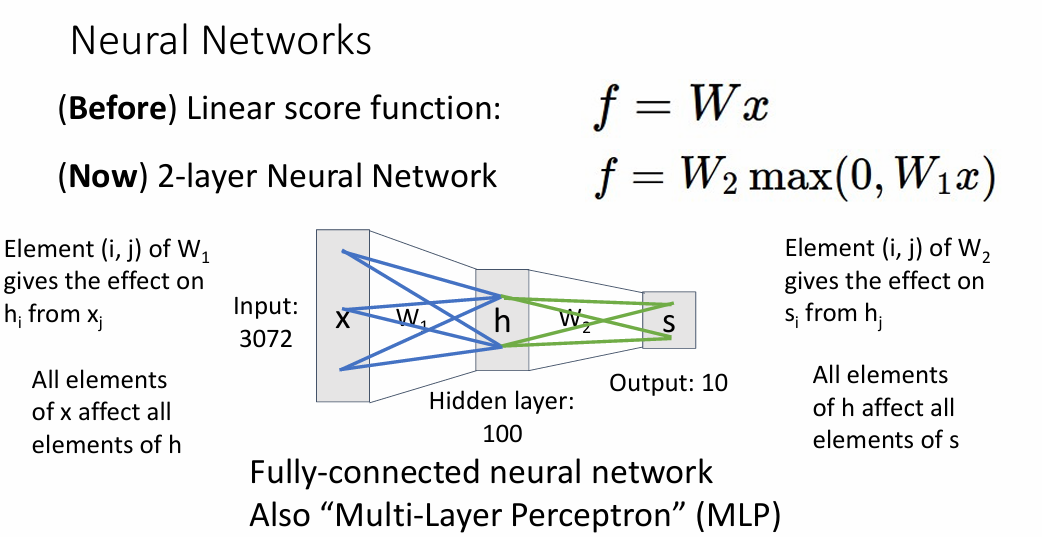
全连接神经网络也叫做多层感知机

因此，计算得分的方式可能会是

1
2
3
4
5
6
7

import numpy as np

h1 = X.dot(W1) # 得到第一层的分数
# 执行Relu, 即 h1 = max(0, h1), 只保留大于0的部分
h1[h1 < 0] = 0
# 经过激活函数后输出到下一层
scores = h1.dot(W2) # 得到分数

上文已提到，不加激活函数实际上做的还是线性变换

可以看到，经过合并后，不加激活函数的结果等价于一个线性分类

激活函数

激活函数的存在就是为了引入非线性，从而可以划分出非线性的决策边界，下面是一些激活函数

简单的实现

ppt中给出了一个简单的使用MSE作为损失函数的两层神经网络

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

import numpy as np
 
# N是训练的batch size; D_in 是input输入数据的维度;
# H是隐藏层的节点数; D_out 输出的维度，即输出节点数.
N, D_in, H, D_out = 64, 1000, 100, 10
 
# 创建输入、输出数据
x = np.random.randn(N, D_in)  #（64，1000）
y = np.random.randn(N, D_out) #（64，10）可以看成是一个10分类问题
 
# 权值初始化
w1 = np.random.randn(D_in, H)  #(1000,100),即输入层到隐藏层的权重
w2 = np.random.randn(H, D_out) #(100,10),即隐藏层到输出层的权重
 
learning_rate = 1e-6   #学习率
 
for t in range(500):
    # 第一步：数据的前向传播，计算预测值p_pred
    h = x.dot(w1)
    h_relu = np.maximum(h, 0)
    y_pred = h_relu.dot(w2)
 
    # 第二步：计算计算预测值p_pred与真实值的误差
    loss = np.square(y_pred - y).sum()
    print(t, loss)
 
    # 第三步：反向传播误差，更新两个权值矩阵
    grad_y_pred = 2.0 * (y_pred - y)
    grad_w2 = h_relu.T.dot(grad_y_pred)
    grad_h_relu = grad_y_pred.dot(w2.T)
    grad_h = grad_h_relu.copy()
    grad_h[h < 0] = 0
    grad_w1 = x.T.dot(grad_h)
 
    # 梯度下降法
    w1 -= learning_rate * grad_w1
    w2 -= learning_rate * grad_w2

这里比较有意思的地方是如何去更新我们的权重矩阵W1,W2

反向传播

求得W1和W2得梯度便可以使用梯度下降法去进行跟新，那么怎么求这两个函数得梯度呢，答案就是去使用反向传播算法。

反向传播算法的核心就是去利用链式求导法则，对于两层或者更多层的神经网络来说，直接求得损失函数对于权重的梯度是一件不太好实现的事情，实际上ppt里面讲解的就是链式求导法则，为了更好的理解链式求导，这里以损失函数为交叉熵函数实现的多分类问题来进行记录。

链式求导

上面构建了一个简单的二层网络，这个网络的工作流程是这样的

• 计算得分

  与之前的线性网络一致，对于输入$X$来说，输出的得分就是 $$ scores = XW_1 + b_1 $$ 不同的是，为了拟合出更多的非线性边界，这里的得分还需要向第二层输出

• 激活函数引入非线性

  假设我们的激活函数为$ReLu$函数，那么 $$ Z(x) = \left{ \begin{aligned} x , x >= 0\ 0, else \end{aligned} \right. $$ 也就是隐藏层h1的输出就是$Z(scores)$

• 经过隐藏层输输入后，我们可以把计算第二层的结果看作之前的线性分类器 即 $$ output = Z(scores)W_2 + b_2 $$ 得到这个output后，可以把结果转为softmax，也就是 $$ y_{pred} = argmax[softmax(output)] $$ 这样就可以使用交叉熵损失函数计算损失

梯度求解

需要额外注意的是，W的梯度dW是在损失函数中学习到的，我们更新W的意义就是去最小化损失函数，最小化损失函数也就是意味着我们的预测越准确，模型所产生的误差越小。

对于一个单层或者多层网络来说，其输入输出、求导方式都是很相似的，下面是一般求解步骤

• 求得损失函数对输出的梯度dout

  在常见的一些损失函数如MSE均值、softmax交叉熵等，可以求得其关于输出的导数，即求得$\frac{dL}{dout}$

• 求得输出关于输入的梯度

  对于输出来说，一层网络的输出就是 $$ output = XW + b $$ 所以，对于，根据链式求导法则，我们就可以很容易的求出损失函数关于输入的梯度

在使用激活函数后，即output其实并不是原始的输出，而是经过激活函数处理后的输出，这也就意味着中间又多了一层关于激活函数的导数，我们以ReLu激活函数为例

一般的，如果不加激活函数，那么我们的求导过程可能是这样的

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

import torch

# 假设我们已经知道损失函数关于输出的梯度
def backward(dout): 
	'''    
	Inputs:
    - dout: Upstream derivative, of shape (N, M)
      - x: Input data, of shape (N, D)
      - w: Weights, of shape (D, M)
      - b: Biases, of shape (M,)
      '''
    # 根据求导公式
    dX = dout.mm(W.T)
    dW = x.T.mm(dout)
    db = dout.sum(dim = 0)
    
    return dX, dW, db

如果在输出层多加了激活函数，那么只需要再多计算一次乘积即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

import torch

def backward(dout): 
	'''    
	Inputs:
    - dout: Upstream derivative, of shape (N, M)
      - x: Input data, of shape (N, D)
      - w: Weights, of shape (D, M)
      - b: Biases, of shape (M,)
      '''
    # 计算dW的梯度
    dW = x.T.mm(dout)
    # 注意，是由输出大于0的部分才有梯度，所以需要进行保留
    dW[out < 0] = 0
    

更一般的，我们会直接对ReLu(x)做求导，从而当输入x发生变化时，我们的ReLu依旧会更加模块化

作业 two_layer_net

讲解一下这个作业中较难的部分

实现forward_pass

可以从函数的参数里面得到需要的参数， 例如W1, b1, W2, b2

1
2
3
4

# Unpack variables from the params dictionary
W1, b1 = params['W1'], params['b1']
W2, b2 = params['W2'], params['b2']
N, D = X.shape

需要额外注意的是这些参数的形状， 我们的训练数据X是NxD的，也就是说，这个训练集中有N个样本，每个样本都是简单的1xD向量，作业为了防止我们出错，还贴心的在注释里面给出了这些参数的形状

1
2
3
4
5
6
7
8

'''
It should have following keys with shape
          W1: First layer weights; has shape (D, H)
          b1: First layer biases; has shape (H,)
          W2: Second layer weights; has shape (H, C)
          b2: Second layer biases; has shape (C,)
    - X: Input data of shape (N, D). Each X[i] is a training sample.
'''

根据这个注释，我们在做矩阵乘法的时候就特别方便

1
2
3
4

# 第一层的输出
hidden = X.mm(W1) + b1
# 经过非线性激活函数
hidden[hidden < 0] = 0

此时，我们就得到了这个二层网络的隐藏层分数

因此，计算输出的总分也是很简单

1
2

# 未经softmax函数处理
scores = hidden.mm(W2) + b2 # raw_scores

到现在，我们就得到了网络的输出分数，现在让我们来梳理一下从图片到预测之间的流程

• 3x32x32数据集

  我们把原始数据集展平为一个一维向量，把若干个这样的向量堆叠在一起，这样就得到了训练集X

• 计算隐藏层输出

  与线性分类器计算分数一样，做乘法运算即可

• 激活函数

  引入非线性，如ReLu, Sigmoid函数

• 输出层

  得到隐藏层分数后计算输出层分数即可

• softmax得到概率

  我们把输出的scores经过softmax后得到近似概率分布，然后概率最高的就是我们网络将图片分类的结果

• 交叉熵损失函数优化

  使用交叉熵函数优化，从而得到之前的W1, b1, W2, b2的梯度，并使用梯度下降法进行学习

也就是说， 在forward_pass中，我们还剩最后两个步骤没有计算出来，下面我们将在nn_forward_backward中计算得出

forward_backward

要想得到损失函数关于W1, b1, W2, b2的梯度， 我们得先求的损失函数，这里使用的是交叉熵损失函数，也就是说，我们需要求得softmax后的分数

• softmax过程

  这部分在A1中已经计算过，在这里在此计算一次。首先根据定义，其实就是每部分exp后除以总的exp和即可。我们的输出scores是一个NxC的矩阵，每一行(dim=1)的含义就是第i个样本(1<=i <=N)在10个类上的总分。例如，假如第i个样本在10个类中cat的分数最大，那么经过softmax后可以近似认为第i个样本是cat的概率最大

  1 2 3 4 5 6 7 8 9 10 11 12

  # 从前向传播中得到分数,注意，这个分数其实是raw_scores scores, h1 = nn_forward_pass(params, X) # 得到分数后softmax化 # 得到每个类别的最大值 max_val, _ = torch.max(scores, dim=1) # 函数返回最大值和最大值的索引 # 除去最大值是防止exp值过大，同时不影响结果 scores_remove_max = scores - max_val.view(-1, 1) # 使用广播机制，不使用也可以 # scores_remove_max = scores - torch.max(scores, dim=1, keepdim=True).values # exp化 scores_exp = torch.exp(scores_remove_max) # 概率化 scores_prob = scores_exp / torch.sum(scores_exp, dim=1).view(-1, 1) # 不使用广播机制同上

• 链式法则

  • dW2和db2

    在求得softmax化后的结果后，我们需要以损失函数的形式表达出来整个解，这里的损失函数是交叉熵损失函数，为了求得损失函数对W2的梯度，使用链式法则会更加简单清晰

    • 交叉熵损失 $$ Loss= -\frac{1}{N}∑log(p_i)+reg⋅(∥W1∥^2+∥W2∥^2) $$ 这里的pi是预测值，也就是我们上面的softmax值，现在，我们可以把求解过程转换一下,即

      $$ \frac{dL}{dW_2} = \frac{dL}{dP} \frac{dP}{dS} \frac{dS}{dW_2} $$

      我们可以来挖掘一下Scores与W2的关系，显然有

      $$ Scores = h_1^T * W_2 + b_2 $$

      怎么求第一项的梯度呢？

      $ \frac{dL}{dP} $的计算公式其实就是对数函数求导，而$\frac{dP}{dS}$的结果就要从softmax公式出发

      $$ softmax(i) = \frac{e^{scores_i}}{e^{scores}} $$

      这个时候就要分当前预测类的类别的情况了，因为对于$p_i$来说，每次都要计算两部分梯度，当计算类别正确时，也就是softmax公式的分子上是含有$e^y_i$，那么此时分子分母都是含有要求导部分；当求其它梯度时，分子上其实就是个常数，求导法则发生了变化。这里推荐一个视频,可能会帮助更好的理解。

      也就是说，对于这部分梯度来说，正确的类别结果-1(正确类别分子上还有求导到部分)，错误类别不需要-1，，而且对这部分求导是因为分母上有需要求导部分。

      而且，每个标签都是One-Hot格式，这样我们就可以求得$\frac{dP}{dS}$

      所以求得$ \frac{dL}{dS}$

      1 2 3

      ds = scores_prob.clone() # NxC ds = ds[range(N), y] -= 1 ds /= N # 注意不要遗漏

      $\frac{dS}{dW}$ = h1(NxH)

      1	dW2 = h1.T.mm(ds) # HxC

      同理也可以求得db2就是 ds

  • dW1和db1

    这里同样使用的是链式法则

    $$ h1 = ReLu(XW_1+b_1) \ Scores = h_1W_2 + b_2 $$

    所以要求 $$ \frac{dL}{dW_1} = \frac{dL}{dS} \frac{dS}{dh1} \frac{dh1}{dW_1} $$ 现在未知参数就是dh1,需要注意的是，因为是ReLu所以小于0的部分会置0

    1 2	dh1 = d_scores.mm(W2.T) dh1[h1 <= 0] = 0 # 小于等于0的不贡献梯度

    这里不清晰的化还可以再加一部分即

    $$ \frac{dh1}{dW_1} = X , h1 >= 0 $$

现在，链式求导的部分我们就求解完了，也是这次作业最难的一部分。

总结

多层感知机成功解决了线性分类不能完成的任务，但是多层感知机也有自身上的缺点，下节来看看大名鼎鼎鼎鼎大名的卷积神经网络！