前言

全连接神经网络面临的问题

在此之前，我们一直是在全连接层神经网络进行讨论，全连接神经网络其实也有许多不便之处

无法理解图像模板

对于之前的所有的有关图像分类实现的任务，对于给定的图片(size:3x32x32)，我们并不考虑图片整体或者图片的一些局部特征是什么样的，而是直接把3x32x32的图片展平为一个一维向量(1x3072)，然后经过一些矩阵乘法，我们就可以得到这个图片的scores
内存问题

3072维的向量似乎还是可以接受的，但是实际上这个图片是非常小的，假设我们使用了一些比较大的图片，那么输入的维度肯定会显著的提升。在进行神经网络全连接后，显然，每一层上都有着巨量的计算，而且为了有更好更复杂的模型，神经网络的层数也会增加，那么在此产生的计算和内存消耗将是巨大的

卷积神经网络

卷积层

卷积神经网络的思路与全连接不同，卷积神经网络更加“尊重”图像的样子，它不会把输入图像进行压缩，而是在乎图像的整体特征，而保留整体特征的一个关键部分就是卷积核

卷积核

卷积核可以保留提取一些图片中相似的特征，只要你了解卷积核是怎么提取图片的特征的，你就会明白为什么

卷积核的计算

卷积核会在原来输入图片的维度上进行计算，假设我们使用的卷积核是3x5x5的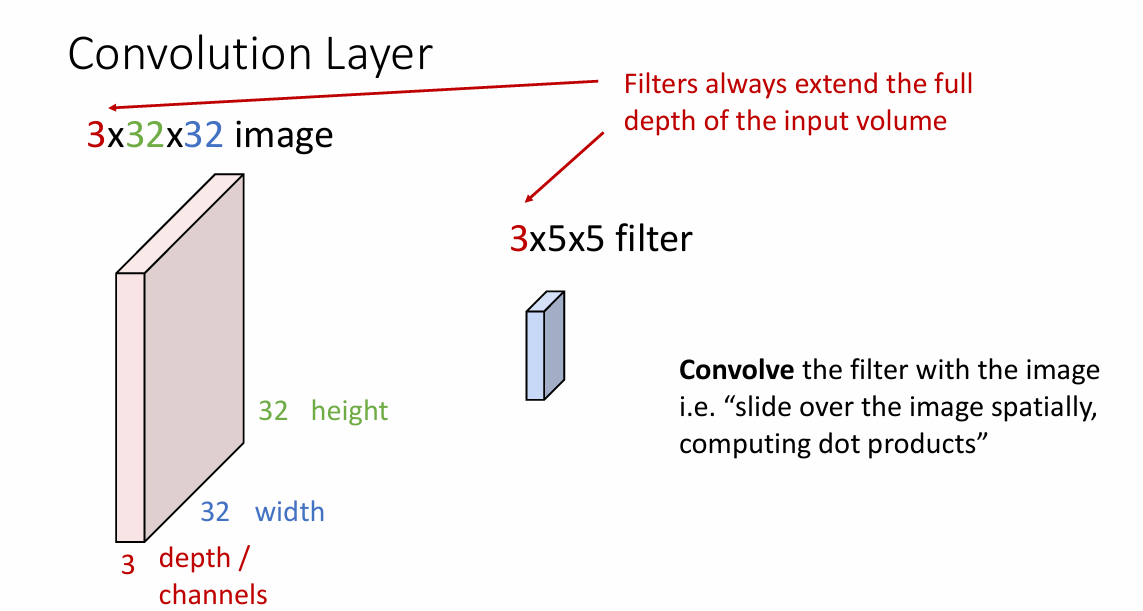

对于图像中每个5x5的部分，我们使用点积去进行计算
多个卷积核的使用

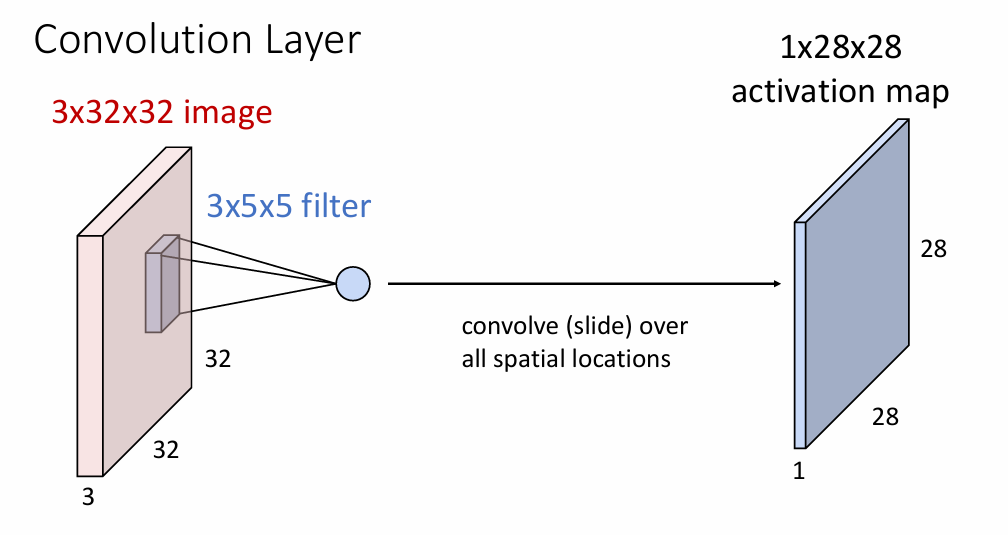
在经过卷积核的计算后，我们得到了一个1x28x28的输出(计算公式后文给出)，更一般的，我们会使用多个卷积核进行卷积，此时卷积核的维度就是Nx3x5x5，那么输出就会是Nx28x28的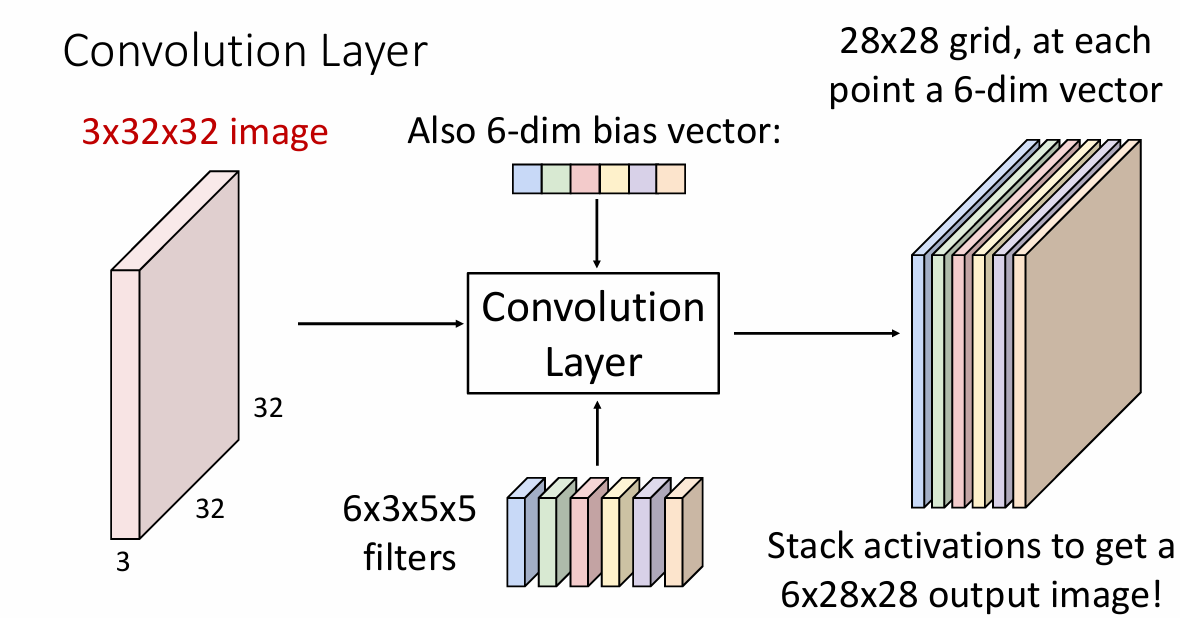

更一般的，对于一批数据，我们会对着一批数据进行卷积操作，此时就变为

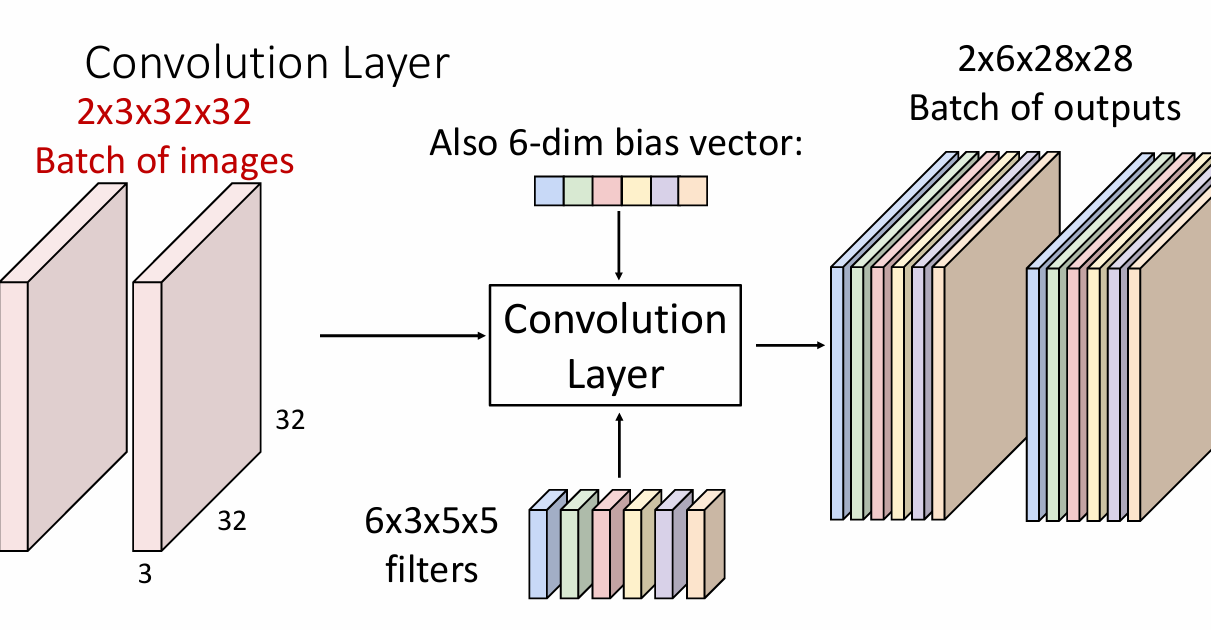
下面是其公式表达形式
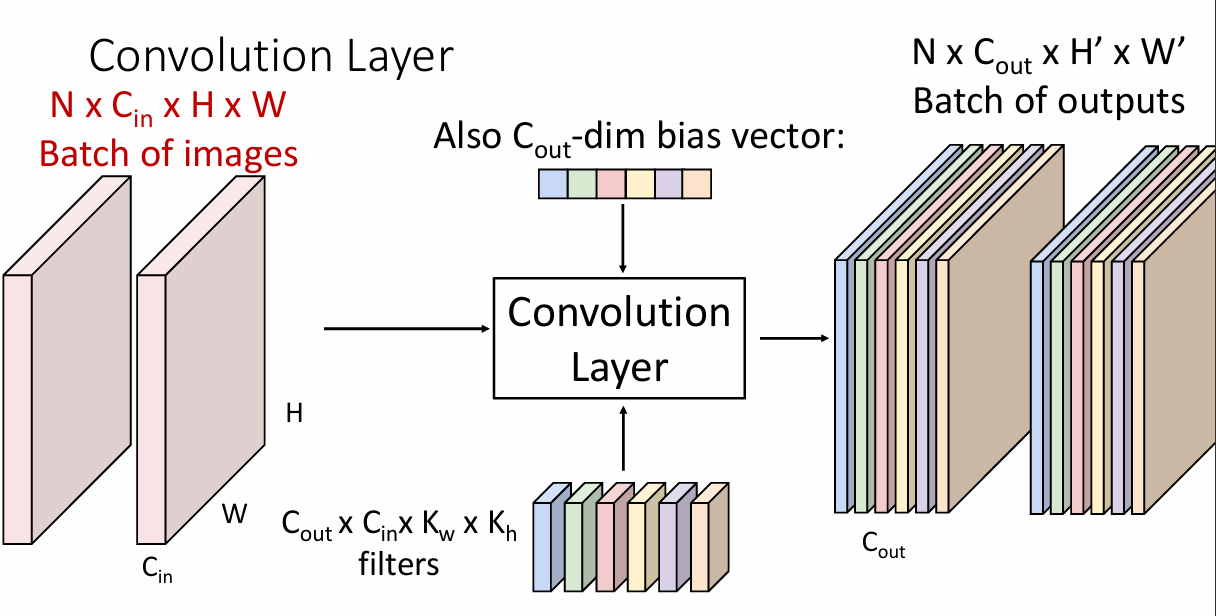
卷积层的堆叠

为了搭建更加复杂的网络，通常会堆积多个卷积层(像之前两层网络一样，在一定范围内层数越多越复杂，能力越高)，此时注意，为了确保引入多个卷积层而不是只是一个卷积层，这里也引入了非线性激活函数(ReLu)

输出大小

卷积的过程就是在原始图片上进行滑动相乘的结果，当使用5x5的卷积核时，输入图片大小为32x32，那么在输入的长上的最后一次运算就是第28, 29, 30, 31 ,32的格子上；同样对于宽也是一样的，这样就可以得到输出图像的特征就是28x28

更一般的，对于输入特征W来说，我们使用大小为K的卷积核进行运算，那么输出特征就是**W-K+1**的，利用这个公式，我们就可以很方便的计算输入特征为32x32时，卷积核大小为5x5时的输出特征。

带来的新问题

经过5x5的卷积核运算后，一个肉眼可见的差别就是输出图像与原始输入图像维数是不同的，当我们使用很多个卷积核后，输出的图像看起来像是降维一样。

为了保持输出图像与输入图像的维度(可能是减少损失的信息)，我们可以使用填充输入图像的方式来保证维度。

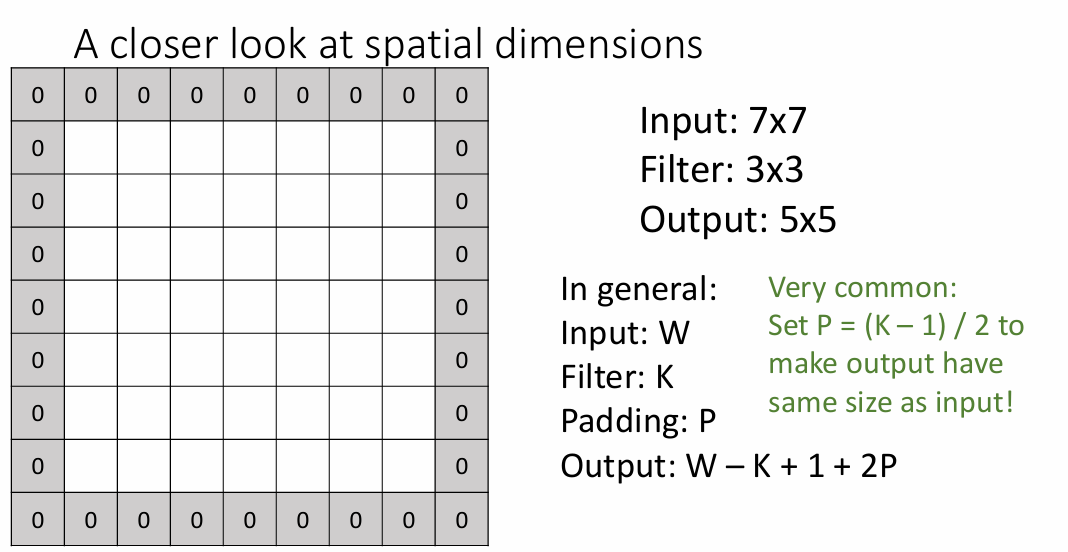
需要填充0的层数p就是(k-1)/2，经过填充，输出的图像大小与输入就有着相同的维度。

不同的步长

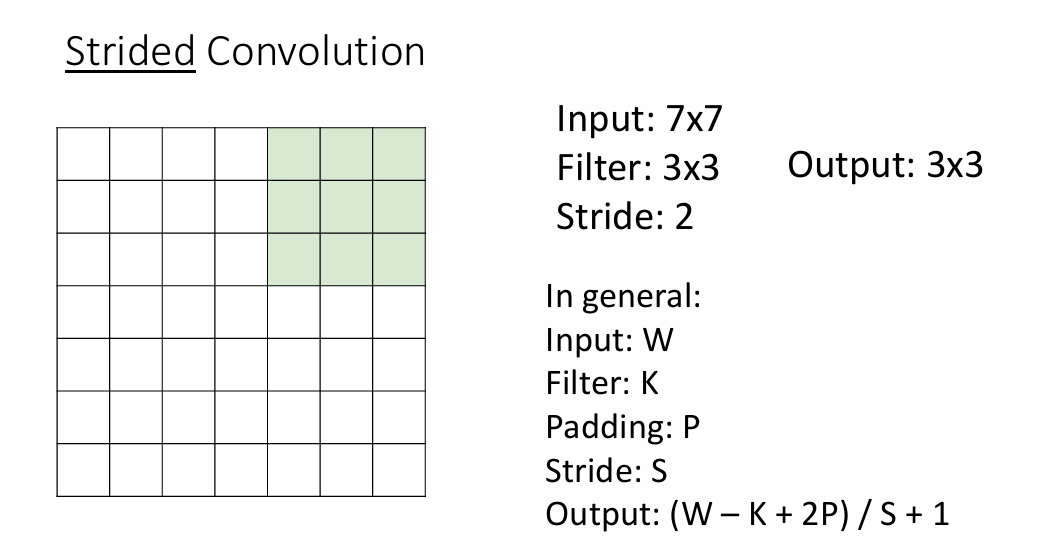
在上面卷积核进行计算的时候，我们都是默认每次卷积的时候都是挨个滑动，事实上滑动的时候也可以跳跃着滑动，也就是说，在原先的基础上，如果每次都是N步去滑动卷积，那么输出的维度就会减小N倍，这个时候我们可以更新我们的计算公式

池化层

池化分为平均池化层和最大池化层，例如，当使用大小为2x2的卷积核进行最大池化的时候，实际上就是对卷积后的每层输出进行特征筛选

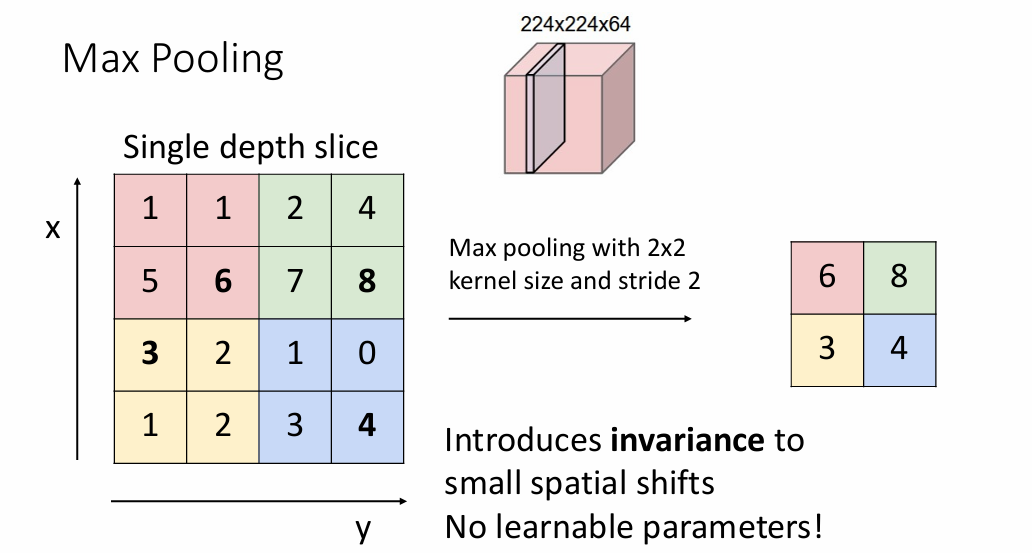
上图是一个使用最大层池化，步长为2的池化层，因为步长的原因，池化后的图片大小会发生变化，使用平均池化也是一样的原理，只需要计算2x2内的均值即可

前向传播

对于给定的数据，怎么实现前线传播的计算呢？假设下面是给定的数据

x, 大小为NxCxHxW，N代表这一批的数据，C表示图片的通道数，HxW是图片的大小
w，大小为FxCxHHxWW，有F个卷积核，每个卷积核大小都是CxHHxWW
b，大小为哦F，表示偏执

现在思考怎么计算经过卷积后的数据out

卷积的过程

首先，我们可以拿出一张图片来进行举例，那么这张图片就是x[i, :, :, :],同时，我们也拿出一个卷积核w[i, :, :, :]。回想一下老师在课堂上举过的例子

这个输出是怎么得到的呢？因为图片是三通道的，所以在每一个通道上都要进行卷积操作，实际上得到的最后输出就是三通道上的总和，那么，对于图片来说，其计算过程就是这样的

1
2
3
4
5
6
7


Hout, Wout = out.shape # 得到输出的size
# 假设步长是stride
for i in range(Hout):
    for j in range(Wout):
        # 这里假设输出和x有着同样size
        # 三个通道的总和
        output[i, j] = (x[:, i:i+k, j:j+k] * w).sum() + b

更一般的，当我们可以进行推广

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


# 输出图片的维度与步长stride和输入的填充有关
N,C,H,W = x.shape
F,C,HH,WW = w.shape
H_out = 1 + (H + 2 * pad - HH) // stride
W_out = 1 + (W + 2 * pad - WW) // stride
for n in range(N):
    for f in range(F):
        for i in range(H_out):
            for j in range(W_out):
                # 计算第n个数据在第f个卷积核上的输出
                out[n, f, i, j] = (x[n, :, i, j] * w[f]).sum() + b[f] # 三通道相乘的和

反向传播求梯度

反向传播求梯度这里其实有点绕，假设我们已经知道损失函数对于输出的梯度dout，那么我们就可以使用链式法则进行求导

out[0, 0, :, :]代表着第1个图片在第一个卷积核上的输出，我们来分析一下它是由哪些部分计算得到的 $$ out[0, 0, :, :] = x[0, 0, :, :] * w[0, 0, :, :] + x[0, 1, :, :] * w[0, 1, :, :] + x[0, 2, :, :] * w[0, 2, :, :] + bias[0] $$ 现在把卷积核的个数拓展到F个，那么求第f个卷积核的输出就是 $$ out[0, f, :, :] = x[0, 0, :, :] * w[f, 0, :, :] + x[0, 1, :, :] * w[f, 1, :, :] + x[0, 2, :, :] * w[f, 2, :, :] + bias[f] $$ 转换为代码就是

1

out[0, f, :, :] = np.sum(x[0, :, :, :] * w[f, :, :, :], axis=0) + bias[f]

需要注意的是，要考虑的是，我们需要学习的参数在哪里参与运算，分层求解其梯度即可。

正则化技术

当网络变得很深的时候，网络通常会变得难以训练，这是因为在我们依赖的方法上的缺点，对于一个很深的网络来说，当前层的梯度来自与损失函数对参数的梯度，而梯度在流动的时候又是依赖于链式法则和反向传播，因此，假设上游梯度：

所有的梯度都是小于1的数

那么在反向传播相乘的时候，很有可能出现梯度消失，即数值过小(nan)
当梯度全部都是大于1的数

那么在反向传播的过程中，多个大于1的数也会导致数值过大而溢出

正则化的作用

why it works?，正则化就是调整数据之间的分布，例如，假设 $$ Y = X_1W_1 + X_2W_2 $$ 而不幸的是，X1可能是一些房屋面积的数据，例如100平米，150平米，而X2有可能是附近的医院个数，例如10,15，显然，两者数据差别有点大，我们可以假设损失函数对于各个数据之间的梯度图，例如

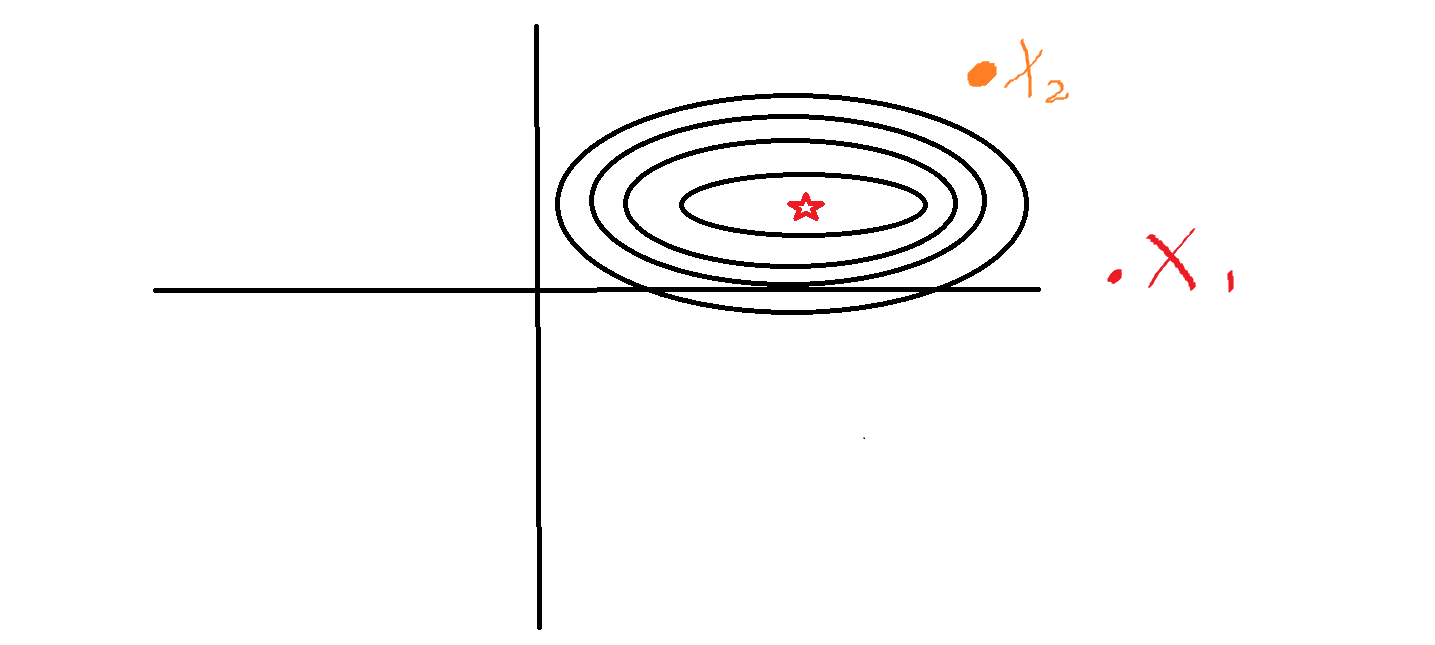
其中X1是数值比较大的数，X2是数值比较小的数，中间的星号就是损失函数最小时X1和X2的取值，可以看到，整个图像的分布就像是一个椭圆形数据，对于X1来说，每次的变化值都要大于X2的变化值，这就导致了每次在梯度下降的时候，很有可能导致下降时候的振荡和无法收敛。

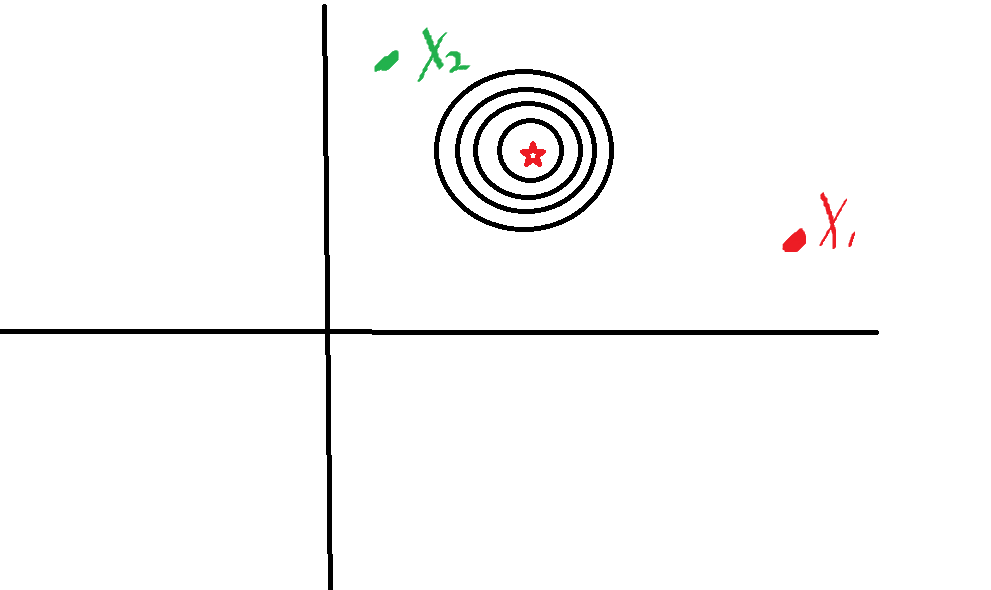
使用正则化之后，可以把数据进行归一化操作，这样对于整个数据分布来说，其形状会更加接近于圆型，这样在梯度下降的时候，对于一些参数learning_rate就可以调整的比较大，同时也可以加快模型的收敛，减少训练时间。

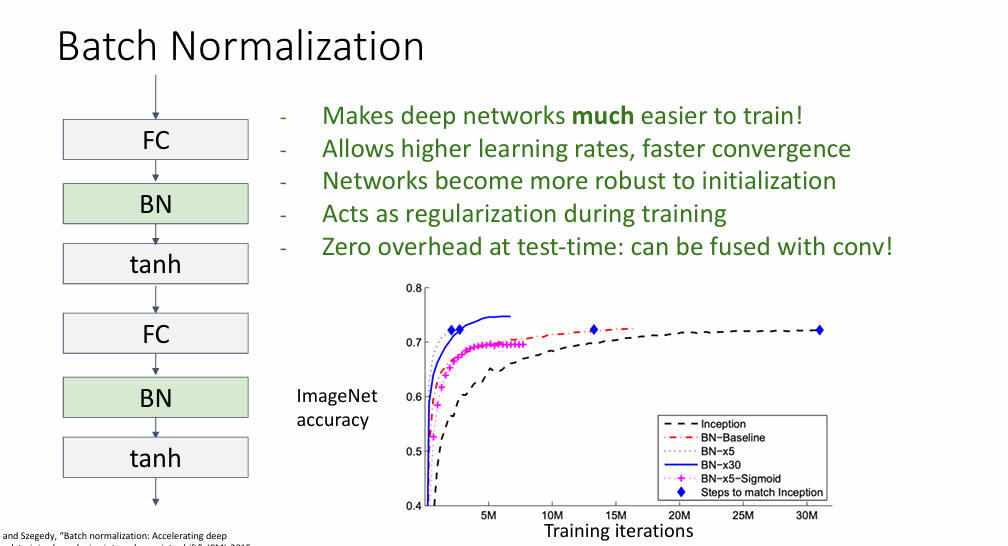
同时，这里的正则化技术有很多，例如batch normalization, layer normalization, xxx normalization，感兴趣的可以自行查阅

批正则化处理的技术一般放在全连接层之后或者卷积层之后，而且是放在非线性激活函数之前

总结

卷积神经网络的组成一般包括：卷积层、池化层和全连接层，其中每个层里面又有各种各样的细节，下次来看一看怎么更好的训练一个网络