前言
继续来看看优化这部分
梯度下降
优化部分主要讲解了与梯度下降以及梯度下降的各种优化版本
虾几霸优化
对于评估一个W参数矩阵来说,需要计算出在这个W下的分类准确率即可。这里的”虾几把“的意思就是随机生成一个参数矩阵W,只要这个矩阵的准确率高于上一次计算的准确率,那么就把当前最优的W更新,然后一直模拟下去,一个可能的算法是这样的
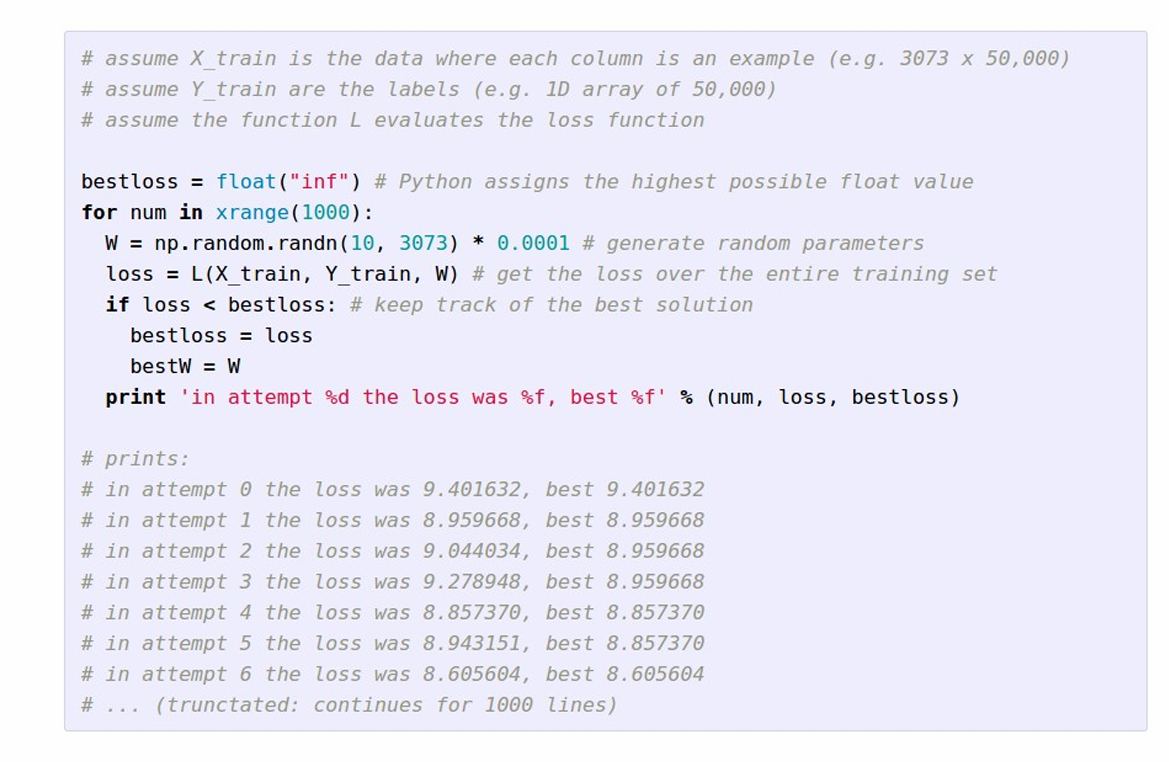
经过这种方法去求得的W在准确率大约在15%,不算太坏,但算不上好!
梯度下降法
在一元函数中,导数可以理解为在这一点上的斜率,在多元函数中,我们使用梯度这个概念来进行导数的推广,实际上,梯度在每一维上的分量就是我们熟悉的导数

沿着负梯度的方向就是目标函数下降最快的方向
因此,对于损失函数来说,我们可以找到W的梯度矩阵dW,然后再对W进行优化,这种方法就是大名鼎鼎的梯度下降

可以看到,这里我们就有了三个未决的超参数
- 怎样初始化
W - 要迭代寻找多少次(
num_steps) - 学习率
learning_rate
其中非常关键的一个参数就是learning_rate,因为最小化损失函数实际上就是去找到目标函数的极小值,在刚开始进行梯度下降时,初始位置在极小值的左边或者右边。下面用$ f(x) = sin(x) $来模拟一下整个过程
-
当学习率很小时
我们总能找到极值, 但是却要寻找很长时间,这是因为每一步都走的特别小,所以寻找要很长的时间,这里假设学习率是
0.1,迭代100次
-
当学习率很大时
学习率很大,这就意味着每一步都走的很大,所以很容易错过最小值,从而造成振荡,下面是学习率为
2的情形
所以,这些参数的选取实际上是在训练神经网络的一些困难之处,而且我们的训练集通常很大,所以每次更换学习率后再训练的代价很大,来说一下这些优化方法!
小批次计算 Mini Batch
在寻找学习率的时候,我们没必要在整个测试集上进行,而是去选择一批样本进行训练,其实这样做也可以减少内存的压力,一个可行的代码是
|
|
这样,在每次训练的时候,我们就可以在小样本上进行迭代训练
|
|
SGD+Momentum
在随机梯度中引入动量的概念,给我们的点增加一个“惯性”的特点

可以看到, 我们的小球确实像物理中的小球那样,在不断的运动着!一个可能的代码是

即先计算速度v,再根据速度v梯度下降
|
|
这个动量的计算公式其实很有意思,它的前身或者本质就是指数加权平均。在使用随机梯度下降时,前面一时刻的梯度似乎不会对后面的梯度造成影响,这就导致随机梯度下降的过程是一个不断震荡的过程,而且很容易陷入局部最小值,而引入指数加权平均时,可以看到,每次梯度的更新都是取决于前面几次的平均值
$$ v_{t+1} = \beta * v_t + (1-\beta)df(x) $$
当$\beta$取0.9时,也就是我们会取梯度的一个样本平均(假设样本为10),这样就把之前计算过的梯度与现在联系在一起,从而避免震荡!
Nesterov Momentum
在ppt中的形式是这样的
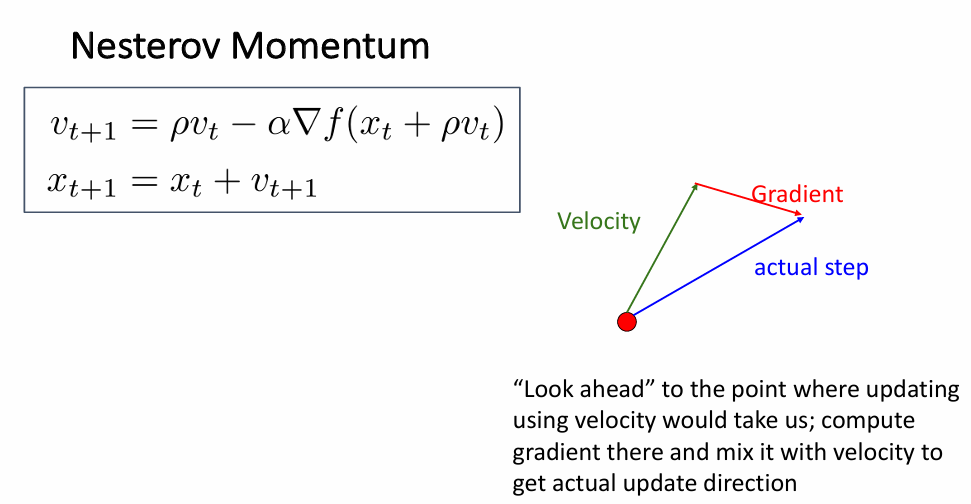
Nesterov Momentum的改进思想在于,它在计算梯度之前,先对参数进行一个“预更新”,即朝动量方向提前迈出一步,这样梯度会变得更加准确。
Nesterov Momentum的更新公式为:
-
预估下一步的位置:
$$ \tilde{\theta} = \theta_t + \gamma v_t $$
-
在预估位置上计算梯度:
$$ v_{t+1}=γv_t−η∇f(θ~) $$
-
更新参数:
$$ θ_{t+1}=θ_t+v_{t+1} $$
同样的,我们还可以使用这种方法去求sin(x)的极小值

使用预估的x求梯度
|
|

AdaGrad
Adagrad 是一种自适应学习率的优化算法,它根据每个参数在训练过程中的历史梯度大小来调整学习率。对于稀疏特征或特征具有不同重要性的任务(如自然语言处理问题),Adagrad 具有较好的效果。
Adagrad 的公式如下:
-
更新梯度累积历史: $$ G_t=G_{t−1}+∇f(x_t)^2 $$
这里 $G_t$是梯度平方的累计和(逐元素累加)。
-
更新参数: $$ x_{t+1}=x_t - \frac{\eta}{\sqrt{G_t + \epsilon}} \nabla f(x_t) $$
- $\eta$ 是初始学习率。
- $\epsilon$ 是一个小值(如 $10^{-8}$),用于避免分母为零。

同样,我们来用sin(x)来模拟一下

可以看到,在这种方法下,“小球”似乎没有它的“物理属性”!
RMSProp
RMSProp是AdaGrad引入指数衰减平均后的优化版本

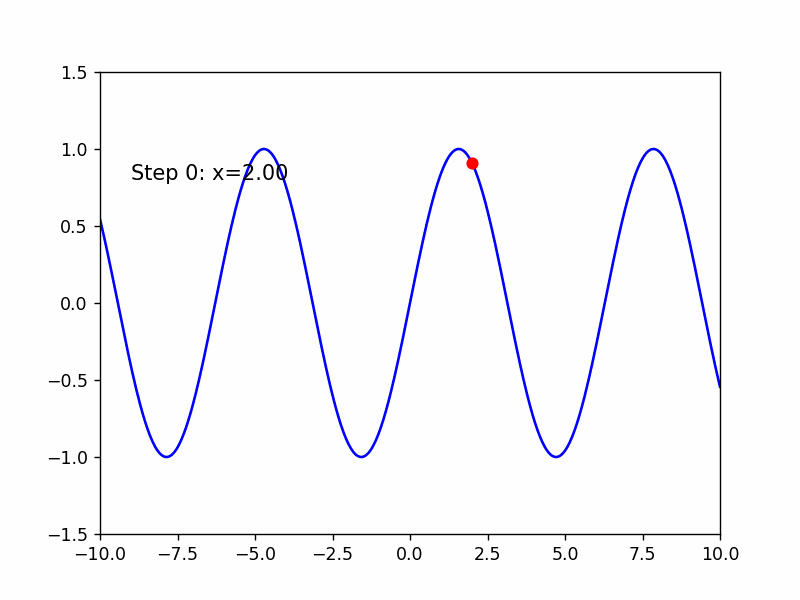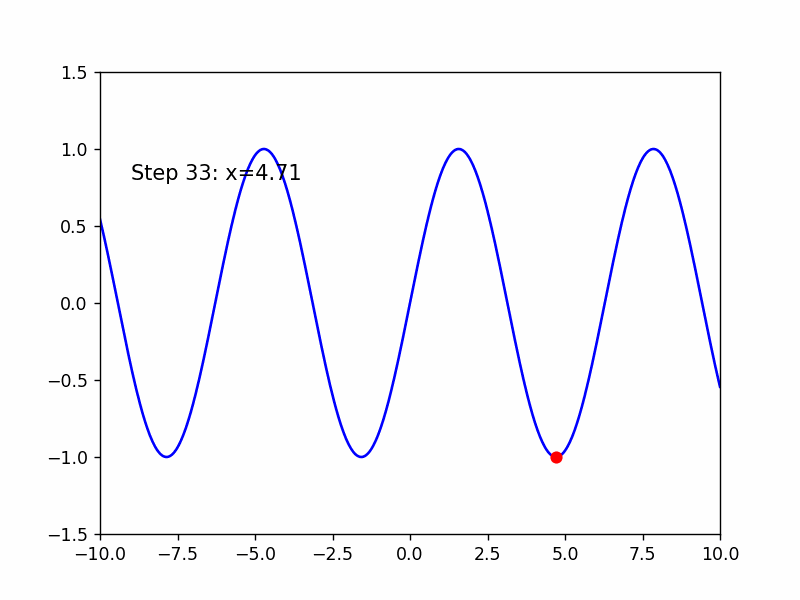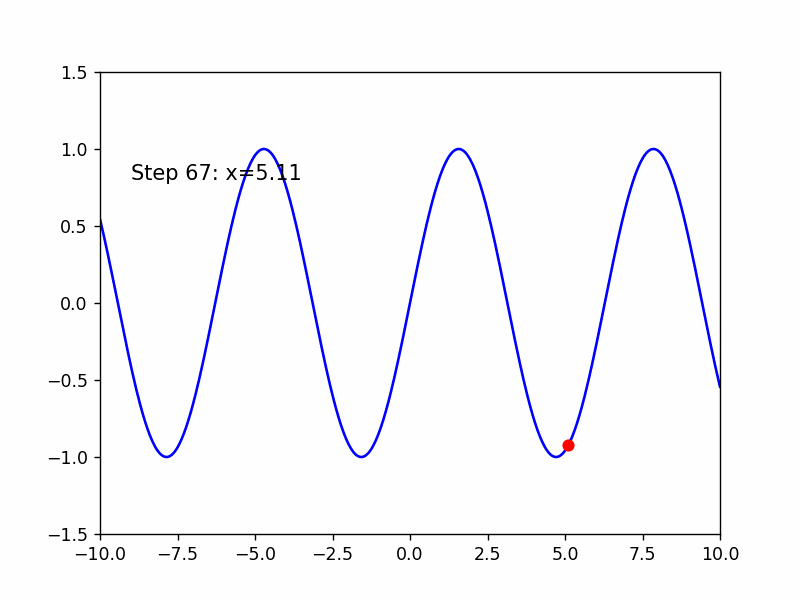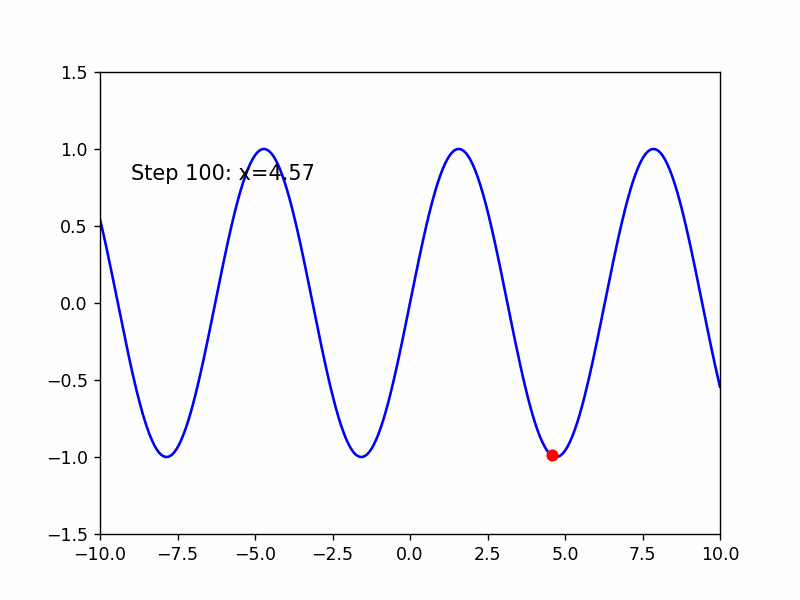
接着使用这种方法来求sin(x)的极小值
有趣的一点是,与AdaGrad采取相同的学习率时,该方法产生了震荡,可能该方法在对学习率的初始值要求较高
Adam
Adma是RMSProp结合了Momentum的版本

继续来寻找sin(x)的极小值点
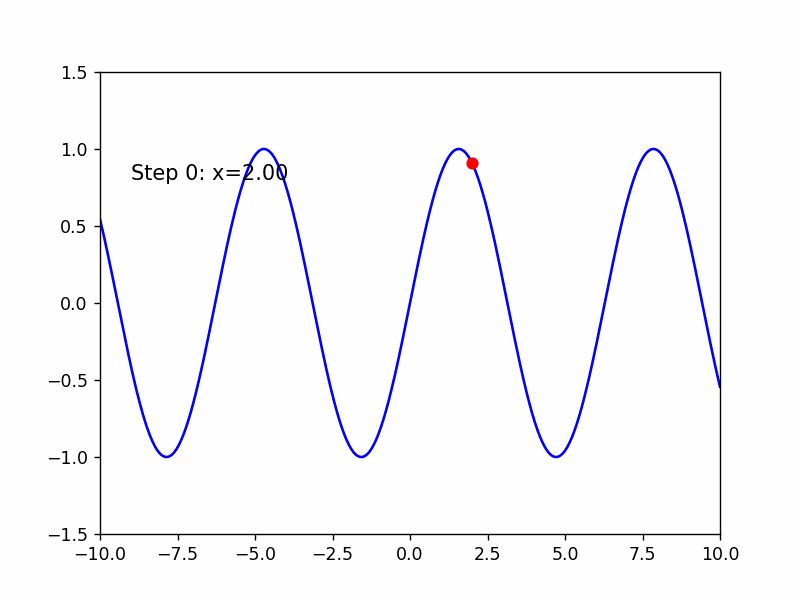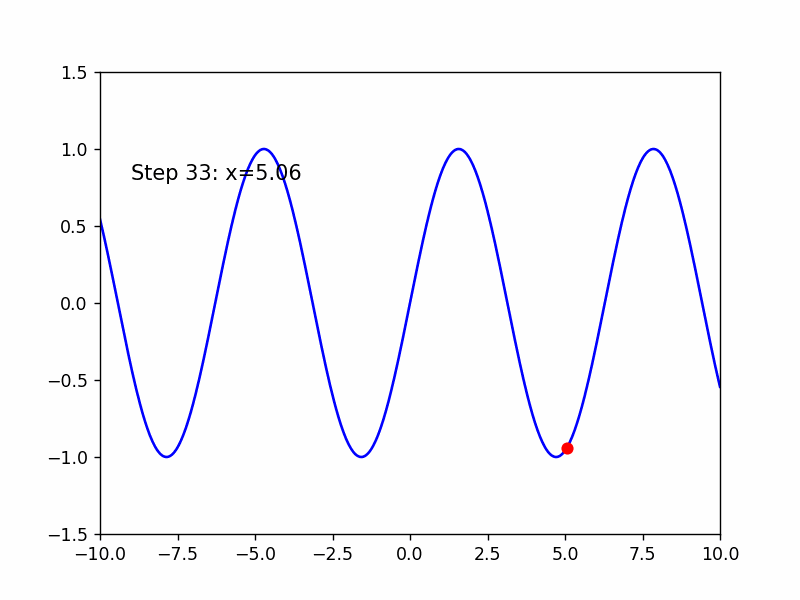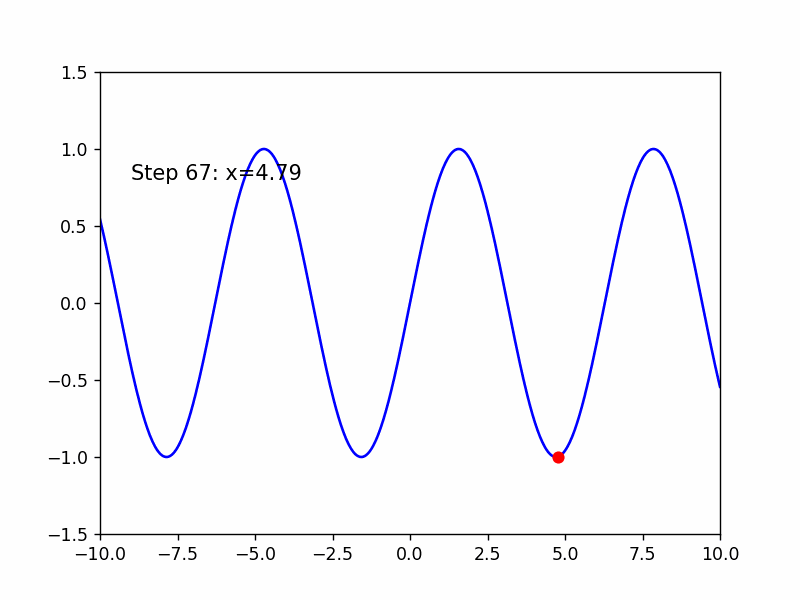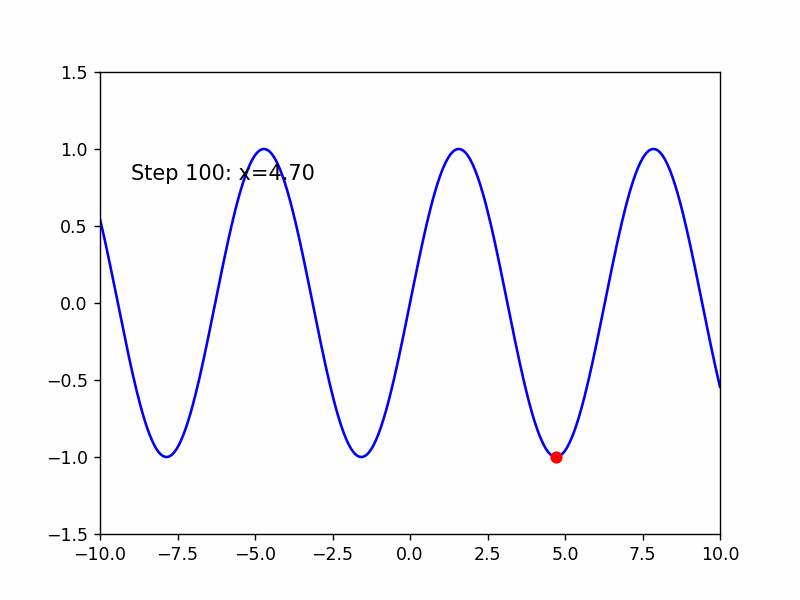
这是老师的经验,超参数的选择是个难点!

总结
在了解这些优化技巧后,一个不错的建议是:优先使用Mini-batch和Adam优化。