前言

本系列是hot100补全计划的二叉树篇，主要包含了力扣(leetcode)的二叉树章节部分的习题，除此之外还会有一些比较著名的但不包含在hot100的二叉树题目。

题目

这道题目是leetcode的第105题，链接在这里(点我)。

意思就是说

给二叉树的先序遍历(根左右的遍历循序)
给定二叉树的中序遍历(左根右的遍历循序)
要求还原出二叉树的原始样子

思路

tips: 对于二叉树和链表来说，使用递归是一类通用的解题技巧

根据先序遍历，显然，第一个结点就是根节点; 根据中序遍历，根节点的左边结点都是左子树，右边节点都是右子树。

也就是说，我们可以根据这个规则来发现一些东西。首先，先序遍历数组preorder的第一个元素一定是根节点，也就是说，每次我们构建根节点，就可以从preorder出发，每次都确定好对应的root坐标；然后，我们就需要正确的划分，哪些值是属于左子树的，哪些值是属于右子树的。

也就是说，给定一个root下表，我们需要找到这个root的左子树和右子树，这该怎么寻找呢？实际上，中序遍历就可以很好的解决这个问题。因为我们已经知道，中序遍历可以很好的划分左右子树，那么，对于preorder[root]元素来说，在中序遍历中，其左边的值就是全部属于左子树，其右边的值全部属于右子树，这样我们就可以很好的确定左右子树的范围。

举个例子

在题目中举例了两个数组，其内容如下

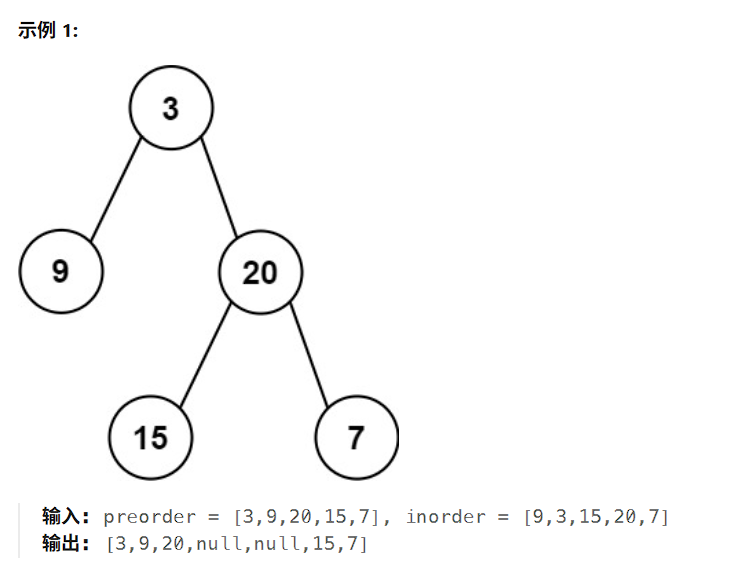
从这两个数组中，我们可以清楚的看到，preorder[0]即为二叉树的根节点，那么从inorder中，可以得出[9]是其左子树，[15, 20, 7]是其右子树的值。但是，得到了右子树，怎么确定右子树的根节点呢？其实，得到左子树的长度后，即长度为1，那么在preorder[0+1+1]即preorder[2]为其右子树的根节点。

所以，我们就得到了一般思路，即根节点要从preorder中进行寻找，左右子树的长度要从inorder中进行寻找。

实现

在寻找某个根节点对应的左右子树的范围一般是这样的，当我们找到一个preorder[root]后，需要在inorder中找到其所在的位置，然后才可以区分左右子树，其过程如下

1
2
3
4
5
6
7


int ans = 0;
for (int i = 0; i < inorder.length; i++) {
    if (inorder[i] == preorder[root]) {
        ans = i;
        break;
    }
}

这样，每次都得进行一次O(N)的寻找，十分耗时，我们可以把inorder存储在一个HashMap中，这样在每次进行寻找时可以以O(1)的时间找到。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55


/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    // 定义一个HashMap来方便快速找到根节点对应的位置
    Map<Integer, Integer> indexOfNode = new HashMap<>();
    int[] preorder;
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder == null || inorder == null) {
            return null;
        }
        this.preorder = preorder;
        // 构建HashMap
        for (int i = 0; i < inorder.length; i++) {
            indexOfNode.put(inorder[i], i);
        }

        // 开始遍历
        return build(0, 0, inorder.length-1);
    }

    private TreeNode build(int root, int left, int right){
        if (left > right) {
            return null;
        }

        // 在中序遍历中，找到对应根节点的位置
        int i = indexOfNode.get(preorder[root]);
        // 也就是说，对于根节点来说，(left, i-1)是其左子树
        // 那么，其右子树范围就是 (i+1, right)

        // 那么，其左子树对应的根节点就是root+1
        // 其右子树对应的根节点就是 root+i-left+1

        // 递归的构建左右子树
        TreeNode node = new TreeNode(preorder[root]);
        // 左子树
        node.left = build(root+1, left, i-1);
        // 右子树
        node.right = build(root+i-left+1, i+1, right);
        return node;
    }
}