前言

递归和树形结构可以说是算法题中比较抽象的地方，尤其是递归。在lab7中，要求我们完成一些对二叉搜索树的一些操作，主要包括：

增加，使用put来增加一个结点
查询，查询某个key是否存在
删除，删除某个key，也是最难的一部分
修改，根据key来修改某个结点

单说可能有些抽象，今天我们就来结合力扣中的一些题目来进行说明。

二叉树的构成

本文中提到的所有二叉树基本是这样的结构

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

即拥有left、right和value属性

插入操作

插入操作put可以说和二叉树的性质有很大关系，因为二叉树的left结点小于root结点，而right结点一定大于root结点，所以，在插入结点时，我们必须按照这个性质来进行插入，不能破坏二叉树的完整性。所以，小于root.val的值应该插入到左子树中，大于root.val的值应该插入到右子树中。

使用递归的方法可以说是很直接了明了，我们来看看这道题目

701. 二叉搜索树中的插入操作

这道题目就是要我们构建一棵二叉树，其实就是完成put操作

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


public TreeNode put(TreeNode root, int val) {
    // 没有根节点，那么我们需要创建一个根节点
    if (root == null) {
        return new TreeNode(val);
    }
    // 需要分清楚是插入到哪个子树上
    int cmp = root.val - val;
    // 需要插入到左子树上
    if (cmp > 0) {
        root.left = put(root.left, val);
        // 插入到右子树上
    } else if (cmp < 0) {
        root.right = put(root.right, val);
    } else {
        root.val = val;
    }
    return root;
}

注意，其实上面的put方法已经包含了对二叉树的修改操作，所以我们来重点看一看二叉搜索树的删除操作。

删除操作

删除操作是一件比较麻烦的事，因为被删除的结点可能还有其它的子节点，为了维护好二叉搜索树的结构，我们就得作出调整，被删除的结点主要包含三种情况。

删除的那个结点没有子节点
删除的那个结点有一个子节点(left or right)
删除的那个结点有两个子节点

我们来跟着slides来看看这三种情况吧，注意slides的大小是按照字典序来进行排序的。

没有子节点的情况

如果我们删除一个没有子节点的结点，假设是glut

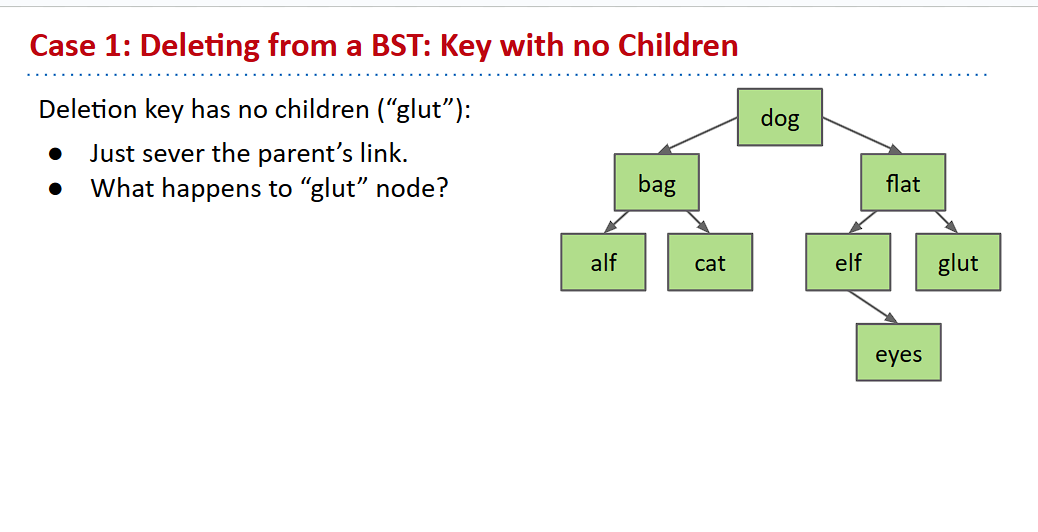
因为这个结点没有子节点，所以我们就不用考虑其它的额外情况，直接把这个结点删除即可。

也就是变成了上面的那样，到时候GC就会自动收集glut

有一个子节点

当有一个子节点时，情况就变得有些复杂了，因为我们需要处理好这个子节点

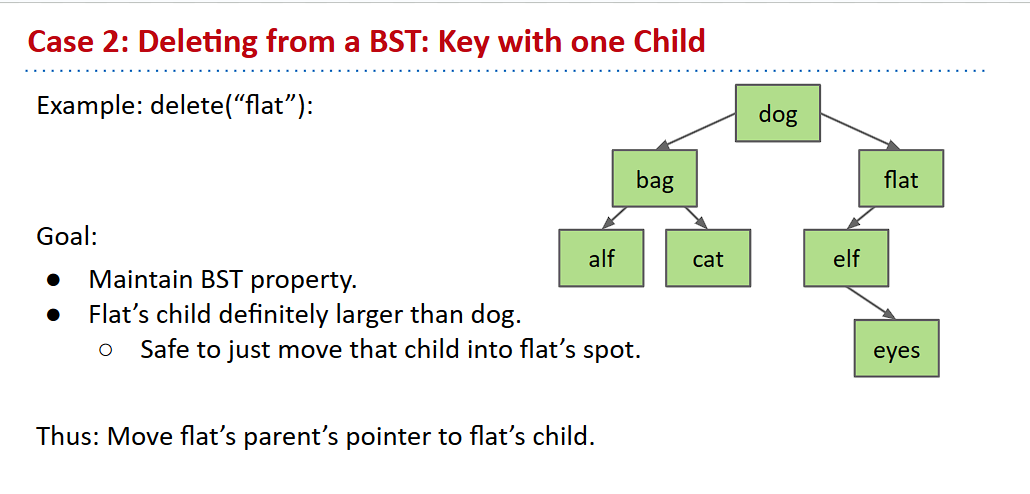
假设我们要删除flat这个结点，也就是说，其结果要变成下面这样

这样也比较直观。

删除两个子节点的结点

这个情况是最复杂的，因为需要考虑重新选择这颗子树的结点来作为根节点。

假设我们要删除dog结点

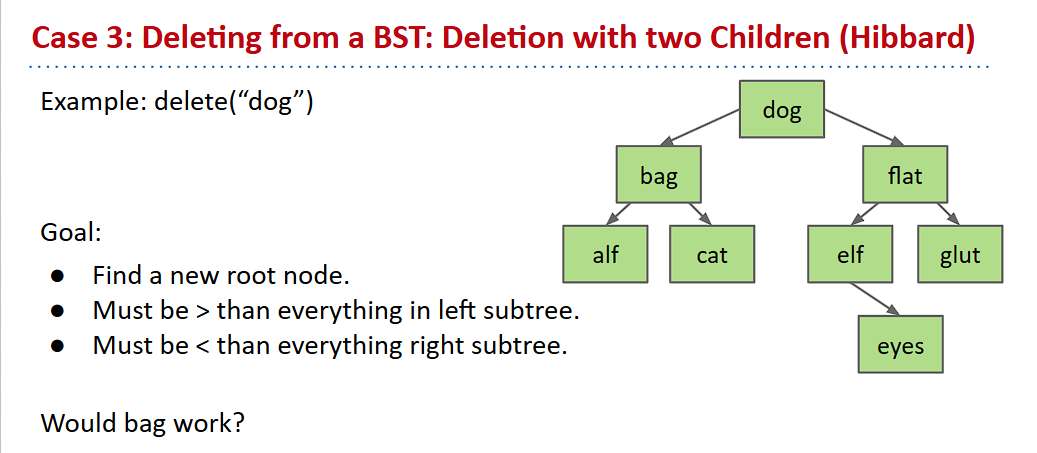
那么，我们就得重新选择根节点，而且还不可以破坏二叉搜索树的结构，也就是说，新的根节点必须是左子树中的最大值，或者是右子树中的最小值。这样，我们就得到了两种方案：

选择左子树的最大值来进行删除，然后作为根节点
选择右子树的最小值来进行删除，然后作为根节点

在上面的例子中，左子树的最大值是cat，右子树的最小值是elf。这种删除方式叫做Hibbard Deletion，感兴趣的读者可以自行查阅。

代码实现

经过分析，我们可以得知，删除之前需要找到子树的最大值或者最小值，这个也不难，根据二叉搜索树的性质可以轻松得出，因为

最大值一定在右子树上
最小值一定在左子树上

找到最小值

1
2
3
4
5
6
7
8
9


/**
	找到最小值
**/

public TreeNode min(TreeNode root) {
    if (root == null) return null;
    if (root.left == null) return root;
    return min(root.left);
}

也就是说，只要找到左子树的终点，也就是没有左叶子结点的那个结点就是我们的最小值。

找到最大值

同理，我们也可以找到最大值

1
2
3
4
5


public TreeNode max(TreeNode root) {
    if (root == null) return null;
    if (root.right == null) return root;
    return min(root.right);
}

接下来实现删除操作，同样的，我们可以和上面的min进行配合。

删除某个node

根据分析，在删除找到最小值后，需要删除，然后进行拼接，最后返回这个新的结点

首先就是要根据给定的某个node来删除它的最小值

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


/**
	删除最小值
**/
public TreeNode deleteMin(TreeNode node, int key) {
    if (node == null) return node;
    // 先进行比较
    if (node.left == null) return node.right;
    node.left = deleteMin(node.left, key);
    return node;
    
}

这样写可能不太直观，我们来画个图看看。

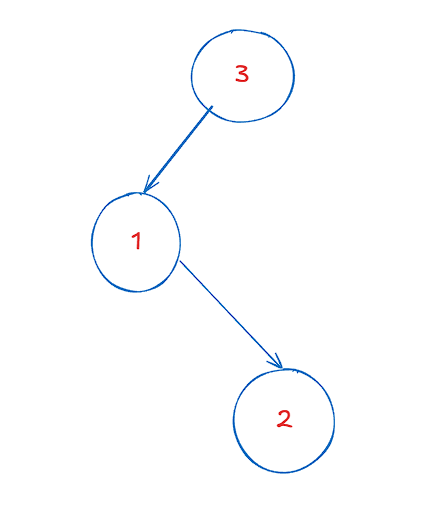
显然，如果我们要删除树中的最小值，即1这个结点，那么删除后的样子就是这样的

即，对root(3)来说，root.left = deleteMin(root.left)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


/**
删除某个值
**/

public TreeNode delete(TreeNode root, int val) {
    if (root == null) return root;
    // 开始进行搜索
    int cmp = root.val - val;
    if (cmp > 0) {
        root.left = delete(root.left, val);
    } else if (cmp < 0) {
        root.right = delete(root.right, val);
        // 找到了这个结点
    } else {
        if (root.left == null) return root.right;
        if (root.right == null) return root.left;
        
        // 有两个结点
        TreeNode t = root;
        // 找到右子树的最小值
        root = min(t.right);
        // 开始进行拼接
        root.left = t.left;
        root.right = deleteMin(t.right, val);
    }
    return root;
}

我们可以把deleteMin理解为，找到并删除最小值后，返回这颗二叉树的根节点。

这样我们就做好一次删除操作了，幸运的是，leetcode上有这道题目，我们来测试一下。

删除二叉搜索树中的节点

可以看到成功通过测试了，我们来总结一下思路

找到某个子树的最小值
把最小值替换，也就是完成deleteMin
递归的去进行搜索

验证是否是二叉搜索树

二叉搜索树还有一道比较有名的题目就是“验证一棵树是否是二叉搜索树”，我们遇到了此类的递归题目，首先要做的就是不要去想的太深，也就是只想象出两层二叉树即可。

验证二叉搜索树

二叉搜索树满足的情况就是其左右子树必须都是二叉搜索树

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {
        return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }

    boolean isValidBST(TreeNode root, long l, long r) {
        if (root == null) {
            return true;
        }
        return l < root.val && r > root.val && isValidBST(root.left, l, (long)root.val) && isValidBST(root.right, (long)root.val, r);
    }
}

总结

二叉搜索树是一种高效的数据结构，但是当插入的结点全部都是有序的时候，二叉搜索树就会退化为链表，这个时候我们就要考虑旋转来保持平衡了。这个以后再看！